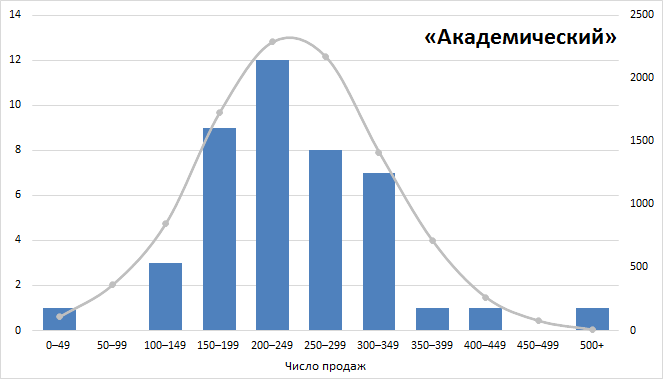
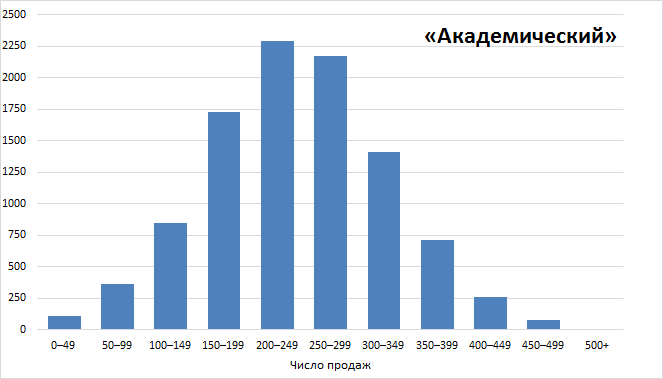
График конверсии с доверительным интервалом
Некоторое время с удовольствием использую более свежую визуализацию конверсии, добавляя к своим диаграммам границы доверительного интервала.
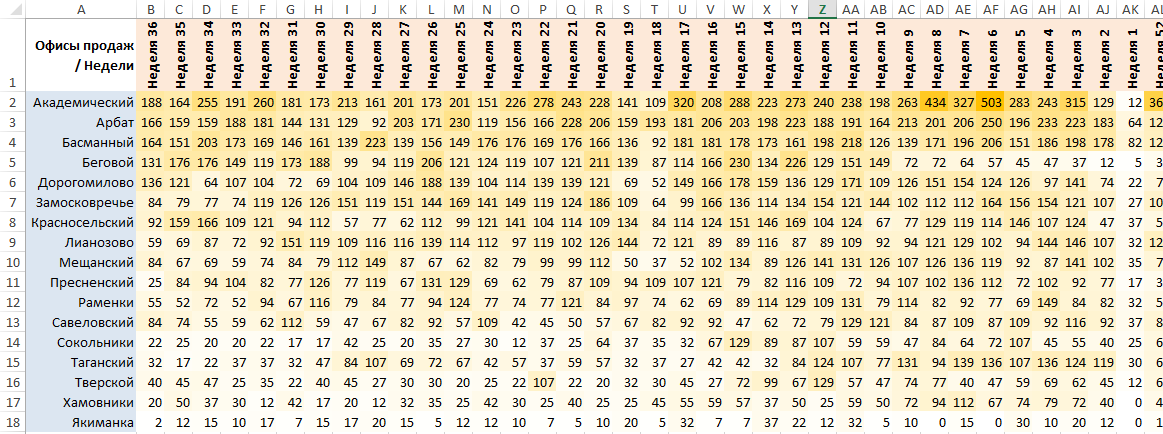
Конверсия офисов продаж
Итак, например, мы оцениваем эффективность работы территориальных офисов продаж. Под эффективностью понимаем отношение числа совершенных продаж к числу заявок (конверсию заявок в продажи, или просто «конверсию»). То есть, если в офисе «Сокольники» за квартал было 19 продаж на 33 заявки, их эффективность будем считать равной 19/33 = 57,6%.


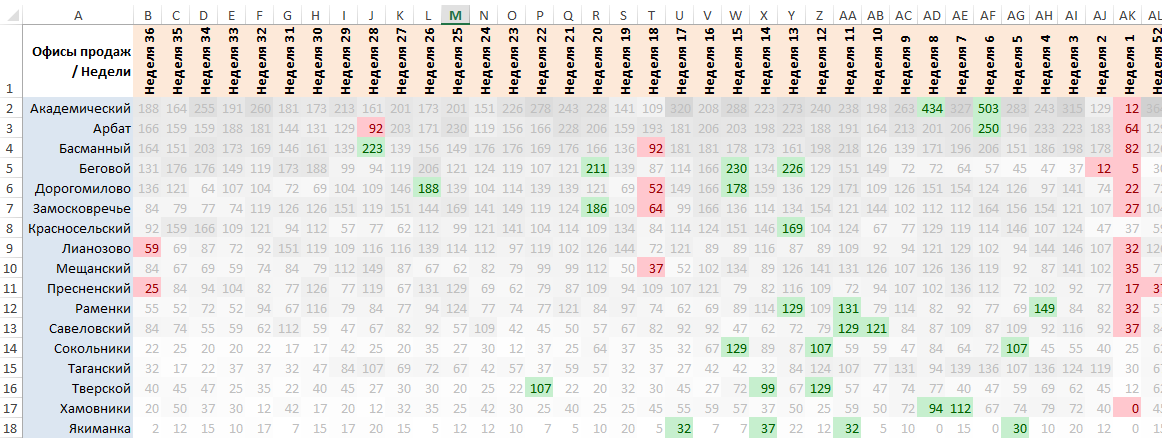
Очевидно, что одни офисы работают эффективнее других: конверсия по офисам меняется от 57,6% до 17,6%. Заметно также, что и число заявок в офисах различно: от 33 заявок в «Сокольниках» до 706 заявок в «Лианозово».
Обычно на этом этапе многие останавливаются, но есть несложный способ воспользоваться понятием «доверительного интервала» или «стандартного отклонения (SD)», чтобы показать то, что, на первый взгляд, не так заметно.
Оцениваем размер выборки и величину SD
Как нетрудно заметить, из-за неравного числа заявок по разным офисам («Сокольники» отличаются в этом смысле от «Лианозово» почти в 22 раза), уверенность в надежности рассчитанной конверсии будет не одинакова. Так, для «Лианозово» результат в 36,1% достигнут на выборке из 706 заявок и может считаться вполне надежным; в «Сокольниках» мы получили результат 57,6% на небольшой выборке в 33 заявки, из-за чего нет уверенности, что, получи со временем последние свои 706 заявок, они бы удержали результат на том же уровне.
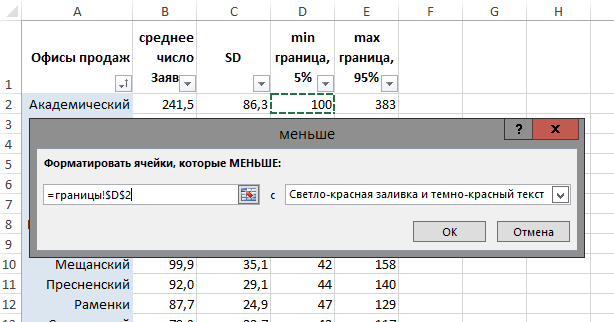
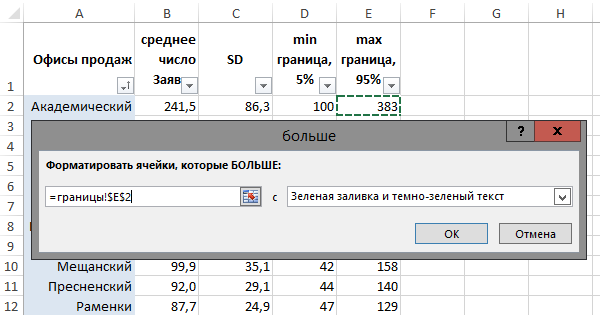
Разумеется, необходимо прикинуть размер доверительного интервала для каждого офиса продаж, исходя из числа заявок, то есть, размера выборки.
Уже знакомая нам формула стандартного отклонения (SD), или σ:

где p — величина конверсии, n — число заявок.
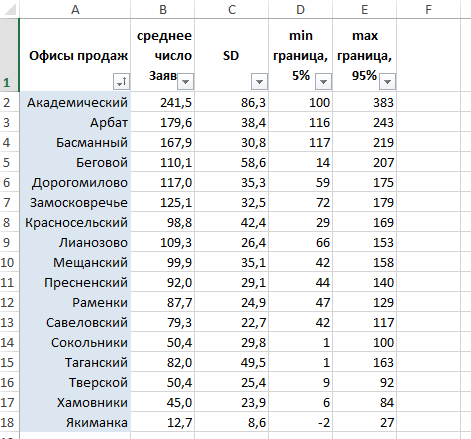
Считаем в колонке E:

Полученная величина стандартного отклонения (SD) показывает погрешность при расчете конверсии, и, очевидно, оказалась выше там, где была меньше выборка. Чем меньше данных, тем менее надежен рассчитанный результат, и тем меньше мы уверены в нашей оценке эффективности соответствующего офиса продаж.
Считаем границы 90%-го доверительного интервала
Дополним нашу таблицу рассчитанными нижней и верхней границей 90%-го доверительного интервала. Другими словами, оценим разброс конверсий по каждому из офисов продаж, так, что с вероятностью 90% мы будем уверены, что истинная конверсия лежит в пределах этого диапазона.

Зная о том, что границы 90%-го доверительного интервала лежат в пределах ±1,645SD, вычитаем и прибавляем 1,645SD для нижней и верхней границ, соответственно. Для «Лианозово» получаем, что их истинная конверсия лежит в пределах от 33,1% до 39,1%. (По-прежнему, в 1 случае из 10 она выходит за границы нашего интервала, но зато в 9 случаях из 10 мы не ошиблись).
Дополняем график, рисуя «свечи»
В Excel 2013 воспользуемся «биржевой диаграммой», указав вместо самого высокого и самого низкого курсов верхнюю и нижнюю границу наших доверительных интервалов, а вместо курса закрытия — рассчитанную вначале конверсию:


Доработанная подобным образом диаграмма не меняет выводов, полученных в самом начале. Однако, для наблюдательного руководителя она ненавязчиво напоминает, что полученные значения конверсий офисов продаж не конечны, и особенно «не конечны» там, где оказались шире границы разброса конверсии.
«Сокольники», предварительно, обогнали «Беговой», однако, если хороший результат «Бегового» надежен за счет узкого интервала, то результат «Сокольников» очень приблизителен, поэтому уверенные выводы возможно делать лишь о части офисов продаж, для остальных — нужно больше данных, а до тех пор их позиции в рейтинге можно считать лишь предварительными, или, как было сказано выше, не конечными.
См. также:
http://italylov.ru/blog/all/ctatisticheskaya-dostovernost-koltrekinga/