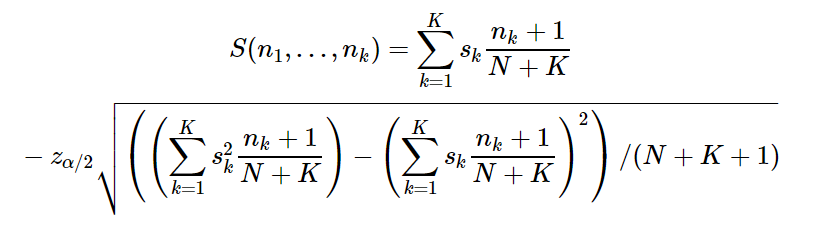В процессе изучения биномиального распределения, обратил внимание, что стандартный способ определения доверительного интервала через ±1,645SD не всегда точен. Грубо говоря, если «решка» выпала меньше, чем в 10 бросках, то, скорее всего, либо вы сделали мало бросков, либо у вас вероятность выпадения «решки» в «заколдованной монетке» сильно невелика; если np < 10, лучше воспользоваться более сложными формулами, дающими более точные оценки при маленьких p или n:

По мнению многих статистиков, наиболее оптимальную оценку доверительных интервалов для частот осуществляет метод Уилсона (Wilson), предложенный еще в 1927 году <...>. Данный метод не только позволяет оценить доверительные интервалы для очень малых и очень больших частот, но и применим для малого числа наблюдений.

Звучит заманчиво. Попробуем разобраться.

Метод Уилсона

Нижняя и верхняя граница доверительного интервала p = 1—α/2 вычисляются следующими формулами:

Формула расчета нижней и верхней границ, соответственно.

где p — наблюдаемая вероятность «выпадения решки», N — число измерений («бросков»), z — z-оценка (например, 1,960 для 95%-го доверительного интервала, или 1,645 для 90%-го).

Пример и калькулятор для расчета

Предположим, нам удалось прослушать 10 рандомных звонков колл-центра, и в 4 из них оператор забыл или поленился уточнить у клиента источник рекламы. Скорее всего, исходя из данной информации, операторы не уточняют источники рекламы в 40% звонков.

Однако, это очень смелое утверждение, ведь наша выборка (10 звонков) откровенно мала: для получения более точной оценки качества работы коллцентра, хорошо бы прослушать больше рандомных звонков (прослушать все звонки, очевидно, невозможно).

Но даже для выборки из 10 звонков, можно рассчитать SD биномиального распределения:

Имеем, SD = 15,49%. С вероятностью 90%, точная оценка качества работы коллцентра (доля звонков, где не выявлен источник рекламы) лежит в диапазоне 40%±1,645SD, или от 14,52% до 65,48%.

Применяя же формулу Уилсона (что уместно, так как np = 4 < 10), границы доверительного интервала уточняются: с вероятностью 90%, истинная доля звонков, где не выявляется источник рекламы, лежит в границах от 19,42% до 64,84%. SD, получается, равно 13,80%.

Калькулятор в Google Таблицах (меню «Файл» — «Создать копию»).

См. также:

«Доверительные интервалы для частот и долей», А.М. Гржибовский, 2008 (стр. 58-59)
Онлайн-калькулятор для 95%-го доверительного интервала
Калькулятор на WolframAlpha.com
Binomial confidence intervals and contingency tests (стр.4-5)
https://influentialpoints.com/Training/confidence_intervals_of_proportions.htm#wils
Wilson score interval на Википедии

Крайне любопытная статья на сайте EvanMiller.org, «Ranking Items With Star Ratings», предлагает продвинутый способ расчета рейтингов, например, по пятибалльной шкале.

(Вообще, судя по интонации автора, история с рейтингами и методиками их расчета не так проста, как может показаться, и он неоднократно к ней возвращается.)

Из того, что удалось понять: во-первых, расчет среднего рейтинга не всегда позволяет однозначно определить место объекта относительно остальных объектов — например, средние рейтинги могут, банально, совпадать. Во-вторых, средний рейтинг не учитывает количество голосов, ведь по идее, чем больше голосов участвует в расчете рейтинга, тем надежнее этот рейтинг.

Простой пример — оценки двух сотрудников:

Осипов — 5, 5, 5, 5, 5, 2, 2, 2, 2, 2. Среднее = 3,50.
Сухонцев — 4, 4, 3, 3. Среднее = 3,50.

Неразрешимая, на первый взгляд, ситуация решается методами байесовской статистики (что бы конкретно это здесь ни значило), вуаля:

Осипов — 2,72.
Сухонцев — 2,63.

Чудесным образом то ли меньшее среднеквадратичное отклонение (0,58 против 1,58), то ли меньшее количество оценок (4 против 10), то ли все они вместе уточнили средний рейтинг Сухонцева, отдав ему предпочтение в несколько сотых.

Формула продвинутого расчета среднего рейтинга

Приготовьтесь, будет немного больно.

Итак, предполагается, что у нас есть K возможных оценок, считаемых по k, каждая оценка стоит s_k баллов («1» — это 1 балл, «2» — это 2 балла и т. д.). Имея N полученных оценок для каждого объекта, по n_k оценок для каждого k, можно посчитать рейтинг каждого объекта по формуле:

Где z_α/2 это 1−α/2 квантиль нормального распределения. Посчитанный рейтинг является нижней границей нормальной аппроксимации байесова доверительного интервала для среднего рейтинга. Принимая, например, α=0,10 (z=1,65), рассчитанный рейтинг S будет означать, что в 95% случаев средний рейтинг объекта будет выше S.

Упрощая, «продвинутый» расчет среднего рейтинга позволяет дать прогноз возможной средней оценки, рассчитываемой традиционным путем. Ну и, следовательно, как показано выше, ранжировать объекты даже при формально одинаковой средней оценке.

Пример расчета продвинутого среднего рейтинга

Вооружившись 2000 оценок по пятибалльной шкале условных территориальных офисов продаж, я посчитал средний рейтинг каждого офиса обычным и «продвинутым» способом.

Среднее 1.0 — средний рейтинг обычный, Среднее 2.0 — средний рейтинг продвинутый.

«Таганский» упал со 2-го на 4-е место по всей видимости, из-за того, что выборка в 66 оценок не дает достаточной уверенности в том, что его средний рейтинг действительно настолько высок, и в 90% случаев его рейтинг прогнозируется выше всего лишь 4,55, что примерно соответствует 4-му месту.

«Академический» формально был на 13-м месте, но, благодаря надежным 249 оценкам, для него прогнозируется, в 90% случаев, средний рейтинг не ниже 4,4, что поднимает его до 10-го места.

У меня сложилось ощущение, что формула более убедительно работает для коротких шкал оценок, как «от 1 до 5» в приведенном примере.

В любом случае, делюсь файлом в Google Таблицах — по идее, он считает рейтинги для всех шкал «длиной» до 100 оценок включительно, позволяет импортировать до 10 000 строк с оценками и корректировать уровень достоверности (90% в нашем примере).

Cм. также

https://www.evanmiller.org/ranking-items-with-star-ratings.html

Продвинутый способ расчета рейтинга в Google Таблицах

Распространенным инструментом оценки качества работы менеджеров отдела продаж является аудит качества телефонных звонков, «прослушка».

Предположим, вы задались целью не просто замерить качество телефонных звонков, но зафиксировать рост этого качества. Например, провели обучение (тренинг) менеджеров, либо предложили новую мотивацию за соблюдение стандартов качества, либо что-то еще.

Логично предположить, что рост качества в первом попавшемся, после тренинга, звонке, не будет однозначно свидетельствовать о росте качества в остальных звонках. Скорее всего, и второй удачный звонок тоже однозначно не подтвердит гипотезу, что качество выросло.

Таким образом, речь будет идти о том, что вам придется прослушать если не все, то, по крайней мере, достаточное число звонков после введенных вами изменений, и число звонков, которые необходимо будет прослушать, на самом деле, можно однозначно рассчитать.

Считаем размер выборки

На 15-й странице работы «Планирование размеров выборки для исследований в бихевиоризме» мне попался подходящий пример 2.4 и формула для расчета таких выборок:

В данном примере рассматривается изменение оценки ACT-теста по математике с 24,5 (дисперсия 8,2) до 26,0 баллов при α = 0,05 и мощности = 0,90.

Для удобства работы, я собрал приведенную формулу в Гугл-таблицах:
Калькулятор размера выборки

Вам остается скопировать файл, и можете подставлять нужные вам значения. Достоверность разумно выбирать от 80% до 95%, значение мощности — от 60% до 80%. Указываете средний балл оценки звонков до изменений, стандартное отклонение (SD) оценки звонков «до», и ожидаемый средний балл оценки звонков после изменений.

Верификация полученных результатов

Важно понимать, что, даже прослушав требуемое количество звонков «после», все равно необходимо проверять наличие статистически значимых различий через калькулятор А/Б-тестов.

См. также:

https://habr.com/ru/post/339798/
https://people.ucsc.edu/~dgbonett/docs/wrkshp/LectureNotes.pdf