Крайне любопытная статья на сайте EvanMiller.org, «Ranking Items With Star Ratings», предлагает продвинутый способ расчета рейтингов, например, по пятибалльной шкале.

(Вообще, судя по интонации автора, история с рейтингами и методиками их расчета не так проста, как может показаться, и он неоднократно к ней возвращается.)

Из того, что удалось понять: во-первых, расчет среднего рейтинга не всегда позволяет однозначно определить место объекта относительно остальных объектов — например, средние рейтинги могут, банально, совпадать. Во-вторых, средний рейтинг не учитывает количество голосов, ведь по идее, чем больше голосов участвует в расчете рейтинга, тем надежнее этот рейтинг.

Простой пример — оценки двух сотрудников:

Осипов — 5, 5, 5, 5, 5, 2, 2, 2, 2, 2. Среднее = 3,50.
Сухонцев — 4, 4, 3, 3. Среднее = 3,50.

Неразрешимая, на первый взгляд, ситуация решается методами байесовской статистики (что бы конкретно это здесь ни значило), вуаля:

Осипов — 2,72.
Сухонцев — 2,63.

Чудесным образом то ли меньшее среднеквадратичное отклонение (0,58 против 1,58), то ли меньшее количество оценок (4 против 10), то ли все они вместе уточнили средний рейтинг Сухонцева, отдав ему предпочтение в несколько сотых.

Формула продвинутого расчета среднего рейтинга

Приготовьтесь, будет немного больно.

Итак, предполагается, что у нас есть K возможных оценок, считаемых по k, каждая оценка стоит s_k баллов («1» — это 1 балл, «2» — это 2 балла и т. д.). Имея N полученных оценок для каждого объекта, по n_k оценок для каждого k, можно посчитать рейтинг каждого объекта по формуле:

Где z_α/2 это 1−α/2 квантиль нормального распределения. Посчитанный рейтинг является нижней границей нормальной аппроксимации байесова доверительного интервала для среднего рейтинга. Принимая, например, α=0,10 (z=1,65), рассчитанный рейтинг S будет означать, что в 95% случаев средний рейтинг объекта будет выше S.

Упрощая, «продвинутый» расчет среднего рейтинга позволяет дать прогноз возможной средней оценки, рассчитываемой традиционным путем. Ну и, следовательно, как показано выше, ранжировать объекты даже при формально одинаковой средней оценке.

Пример расчета продвинутого среднего рейтинга

Вооружившись 2000 оценок по пятибалльной шкале условных территориальных офисов продаж, я посчитал средний рейтинг каждого офиса обычным и «продвинутым» способом.

Среднее 1.0 — средний рейтинг обычный, Среднее 2.0 — средний рейтинг продвинутый.

«Таганский» упал со 2-го на 4-е место по всей видимости, из-за того, что выборка в 66 оценок не дает достаточной уверенности в том, что его средний рейтинг действительно настолько высок, и в 90% случаев его рейтинг прогнозируется выше всего лишь 4,55, что примерно соответствует 4-му месту.

«Академический» формально был на 13-м месте, но, благодаря надежным 249 оценкам, для него прогнозируется, в 90% случаев, средний рейтинг не ниже 4,4, что поднимает его до 10-го места.

У меня сложилось ощущение, что формула более убедительно работает для коротких шкал оценок, как «от 1 до 5» в приведенном примере.

В любом случае, делюсь файлом в Google Таблицах — по идее, он считает рейтинги для всех шкал «длиной» до 100 оценок включительно, позволяет импортировать до 10 000 строк с оценками и корректировать уровень достоверности (90% в нашем примере).

Cм. также

https://www.evanmiller.org/ranking-items-with-star-ratings.html

Продвинутый способ расчета рейтинга в Google Таблицах

Недавно слушал «Вести ФМ», где обсуждались итоги единого дня голосования 8 сентября.

Меня заинтересовала следующая реплика ведущего, с 01:45:05:

Кстати, вот, слушатели из того же Хабаровского края пишут и, примерно, по количеству смсок делятся «50 на 50». 50% считают, что они позитивный выбор совершили, а 50% считают, что стало хуже, и это был негативный выбор. Это, понятно, не социологическое исследование. Ну, вот, просто я вижу десяток, восемь, где-то, смсок, и они примерно пополам делятся. Тоже любопытно.

К чести ведущего, абсолютно корректное замечание-«дисклеймер», что это не «социологическое исследование». И все же, что можно сказать о том, как, в реальности, делятся голоса, если у вас в наличии только 4 смски «за» и 4 смски «против»? Насколько соотношение «50 на 50», полученное на выборке в 8 смсок, подтверждает ровно то же самое распределение голосов в генеральной совокупности?

Считаем в Гугл Таблицах

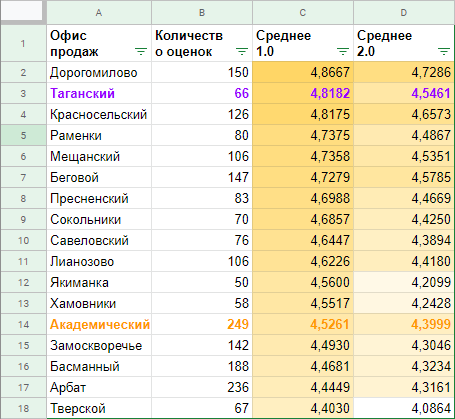
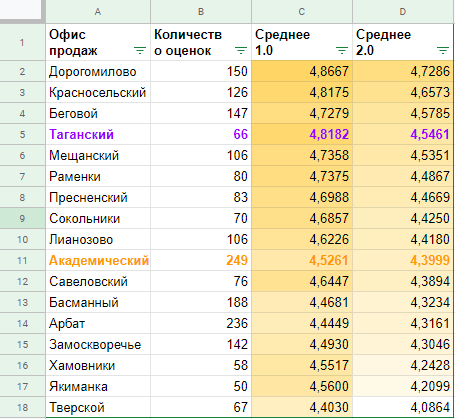
Быстро воспроизводим эксперимент в Гугл Таблицах:

Итак, в тот день 4 человека прислали смски «за», 4 человека прислали смски «против». Логично предположить, что день на день не приходится, и сегодня это были одни слушатели, завтра смски будут присылать другие слушатели, и соотношение сил может быть «3 к 5», «5 к 3», «2 к 6» или «7 к 1» — любое сочетание теоретически возможно. Однако, если мы предполагаем, что взгляды аудитории делятся поровну, то чуть более вероятны сценарии «4 к 4», «3 к 5» или «5 к 3», а сценарии «8 к 0» или «1 к 7», например, менее вероятны.

Технически, мы имеем дело с биномиальным распределением — из 8 смсок мы ожидаем получить 4 смски «за», но не знаем наверняка, сколько их будет. Вероятность получить смску «за» равна 50% (допустим, что ровно 50% аудитории — «за»), в этом случае стандартная ошибка (SD, или σ) биномиального распределения рассчитывалась бы по формуле:

где p = 50%, а n = 8.

Считаем:

Получается, если вероятность получить смску «за» равняется 50%, то стандартное отклонение при выборке в 8 смсок равняется 17,68%!

Что же это означает на практике?

Это означает, что, поскольку имеющаяся выборка (8 смсок) крайне мала, доля случайности в нашем результате «4 „за“, 4 „против“», наоборот, крайне велика, и мы не можем уверенно говорить о строгом распределении голосов «50 на 50» среди всей аудитории «Вести ФМ». Единственное, что мы можем утверждать более-менее точно, это то, что истинная доля голосов «за» лежит в некотором интервале вокруг 50%. И величина этого интервала будет тем шире, чем больше мы захотим быть уверены в его надежности.

Предположим, мы хотим быть уверены в нашем доверительном интервале на 90%. (Оставляем себе право на ошибку в 10% случаев, другими словами). Согласно законам нормального распределения (а биномиальное распределение — это частный случай нормального), данный интервал определяется как 50%±1,645SD.

Такое несложно рассчитать в Гугл Таблицах:

Получается, что истинная доля голосов «за» лежит в интервале 50%±29,08%, т. е. от 20,92% до 79,08%. Примерно вот так это выглядит:

Значит, мы и близко не можем говорить о том, что «слушатели ... примерно ... делятся 50 на 50»! В лучшем случае (даже оставляя 10% на то, что мы ошибемся), мы можем говорить лишь об интервале от 21% до 79%.

Уточнение расчетов

Однако, интервал p±1,645SD тоже является достаточно грубой оценкой. Существуют более сложные, и немного более точные, способы оценить границы интервалов.

Воспользовавшись калькулятором Wolfram Alpha, можно получить следующие границы интервала:

Ну а если хотим, хотя бы, 45-55% получить?

Вот еще интересно: на какого размера выборке, если голоса в ней по-прежнему делятся строго «50 на 50», мы сможем говорить о доверительном интервале, суженном хотя бы до 45-55%?

Рассчитать такое несложно. Если речь идет об интервале 50%±5%, (и мы продолжаем придерживаться уровня уверенности в результате, равном нашим любимым 90%), то 5% должны составлять 1,645 стандартных отклонений (SD). Отсюда, SD = 3,04%. По формуле стандартного отклонения:

откуда несложно найти n = 270,6. Получается, нужно 270-272 смски с распределением голосов строго пополам, чтобы говорить об интервале от 45% до 55% с уровнем уверенности 90%.

См. также

https://en.wikipedia.org/wiki/Binomial_proportion_confidence_interval
Калькулятор на WolframAlpha.com
https://cyberleninka.ru/article/n/doveritelnye-intervaly-dlya-chastot-i-doley.pdf
Cтатистическая достоверность для застройщиков