Крайне любопытная статья на сайте EvanMiller.org, «Ranking Items With Star Ratings», предлагает продвинутый способ расчета рейтингов, например, по пятибалльной шкале.

(Вообще, судя по интонации автора, история с рейтингами и методиками их расчета не так проста, как может показаться, и он неоднократно к ней возвращается.)

Из того, что удалось понять: во-первых, расчет среднего рейтинга не всегда позволяет однозначно определить место объекта относительно остальных объектов — например, средние рейтинги могут, банально, совпадать. Во-вторых, средний рейтинг не учитывает количество голосов, ведь по идее, чем больше голосов участвует в расчете рейтинга, тем надежнее этот рейтинг.

Простой пример — оценки двух сотрудников:

Осипов — 5, 5, 5, 5, 5, 2, 2, 2, 2, 2. Среднее = 3,50.
Сухонцев — 4, 4, 3, 3. Среднее = 3,50.

Неразрешимая, на первый взгляд, ситуация решается методами байесовской статистики (что бы конкретно это здесь ни значило), вуаля:

Осипов — 2,72.
Сухонцев — 2,63.

Чудесным образом то ли меньшее среднеквадратичное отклонение (0,58 против 1,58), то ли меньшее количество оценок (4 против 10), то ли все они вместе уточнили средний рейтинг Сухонцева, отдав ему предпочтение в несколько сотых.

Формула продвинутого расчета среднего рейтинга

Приготовьтесь, будет немного больно.

Итак, предполагается, что у нас есть K возможных оценок, считаемых по k, каждая оценка стоит s_k баллов («1» — это 1 балл, «2» — это 2 балла и т. д.). Имея N полученных оценок для каждого объекта, по n_k оценок для каждого k, можно посчитать рейтинг каждого объекта по формуле:

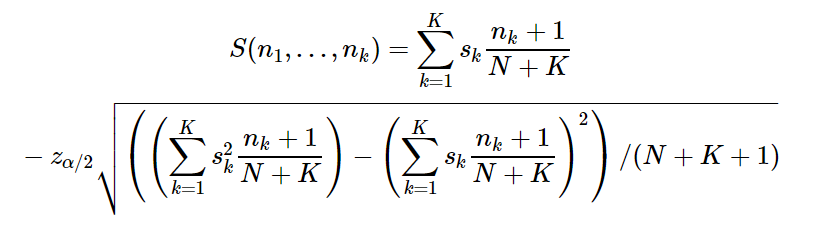
Где z_α/2 это 1−α/2 квантиль нормального распределения. Посчитанный рейтинг является нижней границей нормальной аппроксимации байесова доверительного интервала для среднего рейтинга. Принимая, например, α=0,10 (z=1,65), рассчитанный рейтинг S будет означать, что в 95% случаев средний рейтинг объекта будет выше S.

Упрощая, «продвинутый» расчет среднего рейтинга позволяет дать прогноз возможной средней оценки, рассчитываемой традиционным путем. Ну и, следовательно, как показано выше, ранжировать объекты даже при формально одинаковой средней оценке.

Пример расчета продвинутого среднего рейтинга

Вооружившись 2000 оценок по пятибалльной шкале условных территориальных офисов продаж, я посчитал средний рейтинг каждого офиса обычным и «продвинутым» способом.

Среднее 1.0 — средний рейтинг обычный, Среднее 2.0 — средний рейтинг продвинутый.

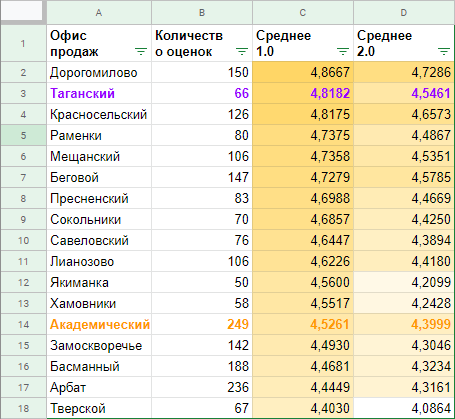
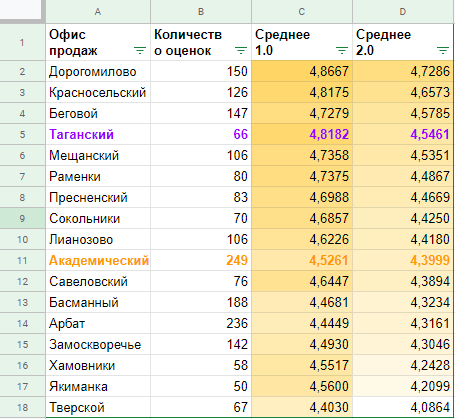
«Таганский» упал со 2-го на 4-е место по всей видимости, из-за того, что выборка в 66 оценок не дает достаточной уверенности в том, что его средний рейтинг действительно настолько высок, и в 90% случаев его рейтинг прогнозируется выше всего лишь 4,55, что примерно соответствует 4-му месту.

«Академический» формально был на 13-м месте, но, благодаря надежным 249 оценкам, для него прогнозируется, в 90% случаев, средний рейтинг не ниже 4,4, что поднимает его до 10-го места.

У меня сложилось ощущение, что формула более убедительно работает для коротких шкал оценок, как «от 1 до 5» в приведенном примере.

В любом случае, делюсь файлом в Google Таблицах — по идее, он считает рейтинги для всех шкал «длиной» до 100 оценок включительно, позволяет импортировать до 10 000 строк с оценками и корректировать уровень достоверности (90% в нашем примере).

Cм. также

https://www.evanmiller.org/ranking-items-with-star-ratings.html

Продвинутый способ расчета рейтинга в Google Таблицах