Проблему, которую помогает решить использование матстатистики, я бы обозначил как «Повысить нельзя уволить» — вот перед нами результаты работы нашего отдела продаж, и назревают вопросы по нашему новому менеджеру Сухонцеву.

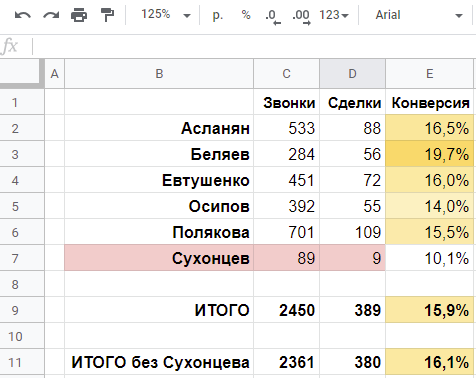
У сотрудника подходит к концу испытательный срок, план по сделкам ему был выставлен как «16 сделок на 100 звонков», поскольку исторически коммерческий директор видел конверсию звонков в сделки на уровне 16,1%.

Сухонцев, хорошо зарекомендовав себя за прошедшие 2,5 месяца работы, имеет 89 звонков и всего 9 сделок, что дает конверсию 10,1%.

«Увольнять,» — решает коммерческий директор.

Внимание, вопрос: справедливо ли решение коммерческого директора? Достаточно ли прошло времени (накоплено данных), чтобы принимать такое кадровое решение? Учтен ли фактор «невезения», и не может ли быть так, что Сухонцев работает не хуже остальных менеджеров, имея, в действительности, конверсию порядка требуемых 16%, но стабильно сталкиваясь с форс-мажорами у клиентов (5 клиентов «отвалились»), «черной полосой» в своей жизни и неудачно вставшей Луной в третьем доме Тельца?

Бросаем игральные кости

Вспоминая пример с бросками монетки, для разнообразия, в этот раз будем бросать игральную кость с 6-ю гранями. Вероятность выкинуть «1» составляет 1/6, или примерно 16,7%.

Математическое ожидание для 89 бросков игральной кости составляет 89 * 1/6 = 14,8 «единичек» (и по столько же «двоек», «троек» и т. д.), но, очевидно, их может быть не только 14-15, но и 12, 17, или, даже, 20. А вот совсем их не быть практически не может (хотя, теоретически, вероятность этого не нулевая).

Работу Сухонцева можно представить как броски игральной кости, где требуемый результат — «единичка»-сделка — выпадает примерно на каждый шестой бросок. Примерно, потому что исторически наблюдаемся конверсия в сделки составляет (без учета работы Сухонцева) 380 сделок на 2361 звонков, или 380/2361 = 16,1%. Математическое ожидание от его 89 «бросков» (звонков) составляет 89 * 0,161 = 14,3 «единичек» (сделок), но, интуитивно понятно, что их может быть чуть больше или чуть меньше.

Если рассчитать (позже узнаем, как) точные вероятности «выпадения» определенного числа сделок на 89 звонков и вывести их на графике, то наиболее вероятное событие («математическое ожидание») в 14 сделок окажется в середине графика, остальные возможные варианты (13 и 15 сделок, 12 и 16 сделок, и т. п.) каждый раз становятся все менее и менее вероятны, из-за чего график приобретает форму колокола:

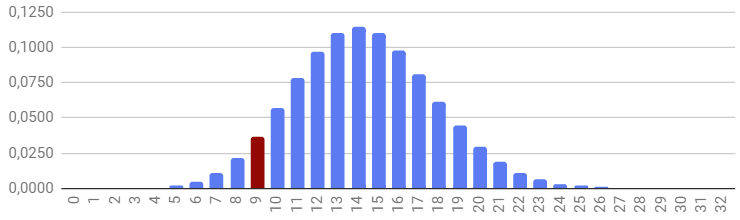
Сказать, что результат в 9 сделок совсем невероятен не получается — какой-никакой, но этот столбик тоже заметен, и даже имеет вероятность в 0,037. Т. е., в 1 случае из 27 он случается, что, может, и маловероятно, но не крайне маловероятно.

Осталось разобраться, как мы получили вероятность «в 1 случае из 27», и как это связать с кадровыми решениями в отделе продаж.

Считаем биномиальное распределение

И в Excel, и в Google Таблицах есть встроенная функция биномиального распределения. Она-то и даст нам ответ на вопрос, пора ли увольнять невезучего Сухонцева.

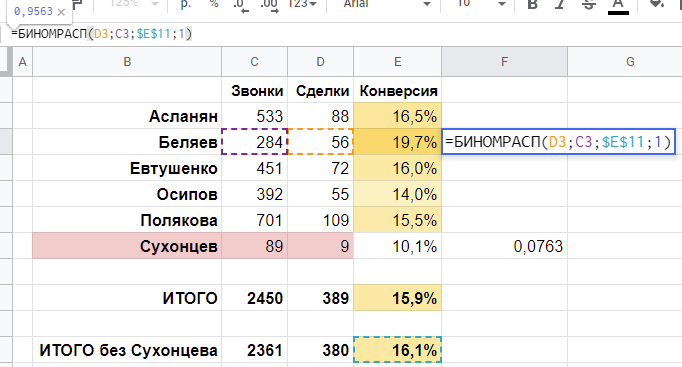
В ячейке напротив его конверсии в 10,1% посчитаем функцию:

=БИНОМРАСП(D7;C7;$E$11;1)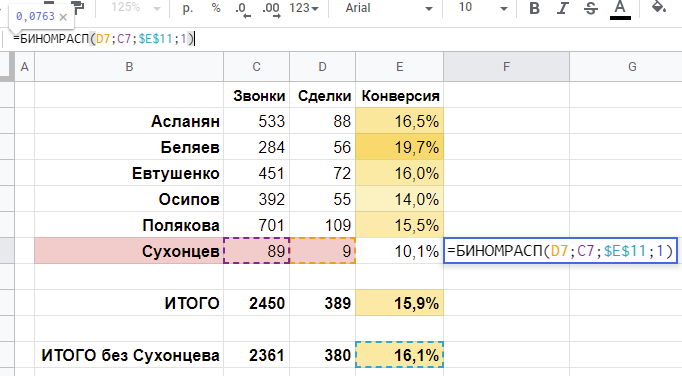

В данной функции указываем по порядку: значение числа успехов (сделок), значение числа попыток (звонков), значение вероятности успеха (конверсия 16,1%). Последний, 4-й параметр, указываем «1».

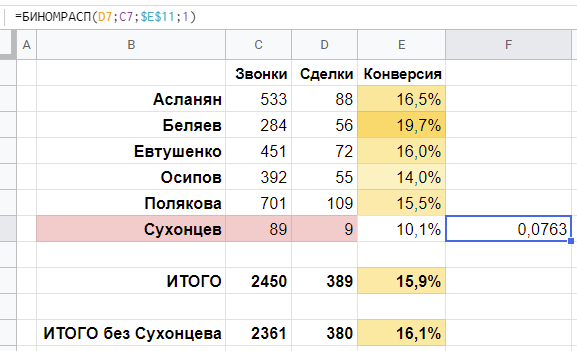
Что за 0,0763 мы получили? 0,0763 — это вероятность получить не более 9 сделок на 89 звонков при вероятности сделки 16,1%. Таким образом, это вероятность получить от 0 до 9 сделок включительно при данных параметрах. Обратно, 1-0,0763 = 0,9237 — это вероятность получить 10 и более сделок.

(Кстати, если 4-й параметр в функции поменять на «0», мы получим вероятность получить ровно 9 сделок).

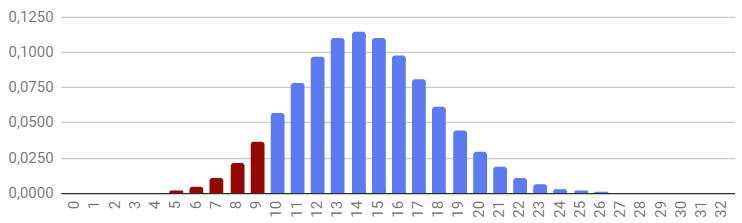
Можно сказать, что, принимая сумму всех столбиков на графике за 1, сумма столбиков «0»-«9» равна 0,0763, или 7,63%. Как видим, гораздо более вероятно попасть в синюю часть колокола нормального распределения, чем в красную (92,37% против 7,63%).

Вывод: вероятность Сухонцеву, работая в действительности с конверсией 16,1%, случайно (возможна «черная полоса», помните?) получить не более 9 сделок из 89 звонков, равна 7,63%. Обратно, 92,37% вероятность того, что Сухонцев получил бы 10 и более сделок. Грубо говоря, 7,63% за то, что ему не повезло, а 92,37% за то, что одним невезением тут не обошлось, и, скорее всего, он работает с конверсией ниже 16,1%.

Таким образом, если для коммерческого директора уровня 90% уверенности достаточно, то Сухонцева можно увольнять с испытательного срока — менеджер, действительно, не выполняет план. Если же нужен уровень 95% уверенности, то данных пока недостаточно, и желательно понаблюдать чуть дальше.

Какой же уровень уверенности выбрать? Правильного ответа здесь не существует.

Если его выбрать слишком низким, то мы можем случайно уволить хороших менеджеров, зато не придется терять сделки, продолжая работать с плохими.

Если выбрать его слишком высоким, то слишком долго придется копить данные для принятия математически обоснованного решения об увольнении плохого менеджера, зато и меньше вероятность случайно уволить хорошего. По моему мнению, уровень 90% для описанного кейса оптимален. Сухонцева можно увольнять.

Постойте, а что с 19,7% Беляева?

Действительно, если существуют «плохие» менеджеры, для которых с вероятностью 92,37% конверсия ниже требуемых 16,1%, то, логично, могут существовать и «хорошие».

Наше внимание обратили на себя 19,7% конверсии Беляева. За полгода работы он сделал 56 сделок на 284 звонка, при прогнозируемых 0,161*284 = 46 сделках. Могло ли ему везти эти полгода? Могло ли быть так, что, работая в действительности как все, с конверсией 16,1%, он случайно получил больше сделок, чем прогнозировал коммерческий директор?

Функция биномиального распределения дает результат в 0,9563 — то есть, с вероятностью 95,63%, работая как все, он бы получил не более 56 сделок... но он и не сделал более 56 сделок! Он сделал ровно 56!

Доработаем функцию, пересчитав ее для 56-1 = 55 сделок:

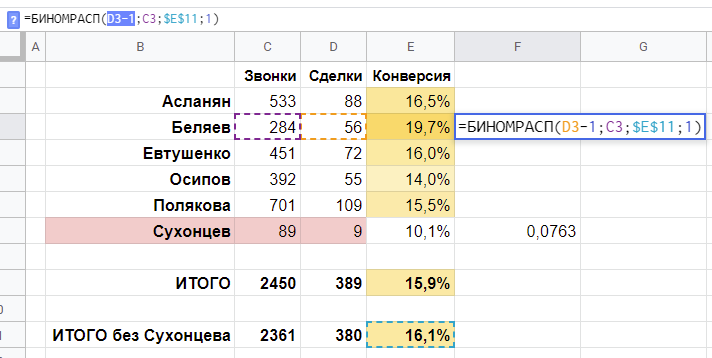
Для 55 сделок результат получился 0,9402. То есть, с вероятностью 94,02% Беляев (работая с конверсией 16,1%) получил бы не более 55 сделок. Получается, вероятность получить более 55 сделок равна оставшимся 5,98%! Получается, наш Беляев попал в кусочек своего колокола распределения, только с другого конца, и вероятность попасть туда составляет всего около 6%.

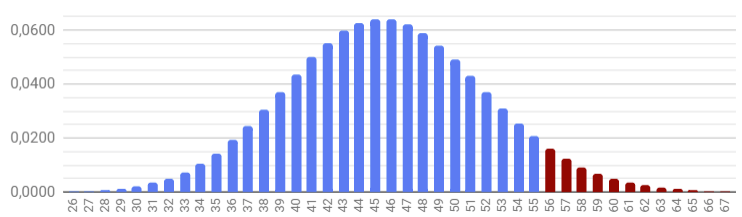
Коммерческий директор уже решил, что, прежде чем принимать кадровые решения, он хочет быть уверен в результатах на 90%. Но в результатах Беляева он уверен на 94,02%! Значит, остается всего 5,98% на то, что Беляеву повезло.

Значит, либо ему так повезло, хотя он, в действительности, работает как все (с конверсией 16,1%) и недостоин большей зарплаты, либо, он работает с конверсией выше 16,1% и будет справедливо вознаградить его.

6% явно проигрывают 94%, поэтому, Беляев получает повышение.