На днях пришел в голову такой пример: предположим, подрядчик жалуется на плохую связь «в каждом пятом» звонке.

Наша задача проверить, справедлива ли гипотеза, что 20% звонков имеют проблемы со связью. Причем, как всегда, мы не просто сделаем 100 тестовых звонков (на это у нас нет ресурсов), а сформулируем нулевую гипотезу, альтернативную гипотезу, и проверим ее с заданным уровнем достоверности.

Выдвигаем гипотезу и определяем уровень достоверности

Нулевой гипотезой (H₀) пусть будет предположение, что со связью все в порядке, или, по крайней мере, проблемы встречаются реже, чем в 20% звонков.

Альтернативной гипотезой (H₁), которую мы будем проверять, пусть будет предположение подрядчика, что в каждом пятом звонке наблюдаются помехи. То есть, по крайней мере, в 20% звонков есть проблемы со связью.

Уровень достоверности — это наша уверенность в результатах эксперимента. Чем он выше, тем больше придется сделать проверочных звонков, поэтому мы заложим 1% на возможную ошибку, и выберем уровень достоверности в 99% (1%, что, если даже эксперимент не подтвердит проблем со связью, они, в действительности, могут быть).

Cобираем формулу для расчета выборки

Предположим, цель эксперимента — опровергнуть альтернативную гипотезу H₁ («есть проблемы»), подтвердив нулевую гипотезу H₀ («все в порядке»). Чтобы сделать это, нам будет достаточно продемонстрировать N подряд успешных звонков без признаков проблем со связью, при этом допуская вероятность, равную или меньше 1%, что нам просто повезет, и, при наличии, в действительности, проблем с оборудованием, они случайно не проявят себя ни в одном из N звонков.

Из предположения подрядчика вытекает, что 80% звонков не имеют проблем. Вероятность отсутствия сбоев в N звонках подряд равна 0,80^N. Нам нужно подобрать минимальное N, при котором вероятность упадет до 1%: 0,80^N = 1%

Получается, нам нужно вычислить логарифм 1% по основанию 80%!

Загружаем в Гугл Таблицы:

Формула для ячейки C5 будет выглядеть как

=LOG(1-C2;1-C3)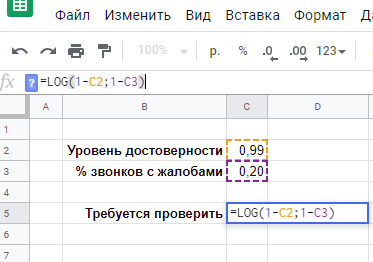

Нужно сделать 20,64 звонка. (Проверяем: 0,80^20,64 = 0,9995%, идеально.)

Остается только добавить округление:

=ОКРУГЛВВЕРХ(C5)

или сразу

=ОКРУГЛВВЕРХ(LOG(1-C2;1-C3))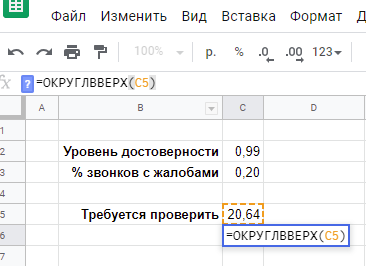

Проверяем гипотезу

Если альтернативная гипотеза H₁ нашего подрядчика верна, и мы испытываем проблемы со связью в каждом пятом звонке, то, вероятность не заметить проблем в 21 тестовом звонке подряд составляет порядка 1%. Иными словами, либо это крайне редкое совпадение (1%), либо альтернативная гипотеза о проблемах в 20% звонков неверна (99%), и мы оставляем нулевую гипозеу H₀. С вероятностью 99% мы уверены, что проблем со связью не наблюдается.