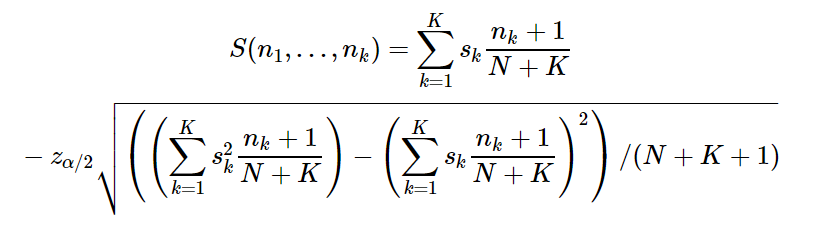В последнее время много размышлял о том, как, с точки зрения статистики, можно кратко оценить или описать любую совокупность или выборку. Пришел к выводу, что, глобально, существует 3 уровня понимания выборки.

Пруд с золотыми рыбками

Для примера, возьмем мой любимый пруд с золотыми рыбками. Вот такой:

100 золотых рыбок. (На самом деле, рыбок-клоунов, но не важно.)

Предположим, мы знаем вес каждой рыбки в граммах (или длину в миллиметрах, не имеет значения в данном случае):

Имея такую выборку, что мы можем сказать о наших рыбках в общем? Как кратко описать множество этих рыбок так, чтобы стало немного понятнее, с чем мы имеем дело с точки зрения статистки?

1-й уровень понимания. Среднее значение.

Проще всего было бы рассчитать среднее значение веса рыбок — в нашем случае получилось бы 96,70 г. Тогда, на первом, самом базовом уровне понимания, мы бы сказали:

— В нашем пруду водятся золотые рыбки. Их средний вес равен 96,70 г.

Верное ли утверждение? Верное. Действительно, несмотря на то, что попадаются и рыбки весом 26 г, и рыбки весом 175 г, средний вес рыбок равен 96,7 г.

Достаточно ли данной информации? Как минимум, ее достаточно, чтобы представить множество из ста рыбок по 96,7 г каждая, и, приблизительно, это дает понимание о качестве рыбок в нашем пруду. Вооружившись удочкой, мы бы шли ловить таких рыбок.

Однако, этого будет недостаточно, чтобы понять, например, как сильно рыбки различаются между собой. Потому что случайно выловленная рыбка может весить гораздо меньше, чем 96,7 г. И тут мы подошли бы к следующему, более углубленному, уровню понимания.

2-й уровень понимания. Стандартное отклонение.

Чуть более образованный человек не удовлетворился бы информацией о том, что средний вес рыбок равен 96,7 г. Он обязательно пошутил бы про «среднюю температуру по больнице» и уточнил бы, а как сильно различаются рыбки по размеру между собой?

Такое различие называлось бы стандартным отклонением (или дисперсией). Оно описывало бы величину отклонения веса случайной рыбки от среднего веса всех рыбок.

Проведя несложные вычисления, мы бы узнали, что, в среднем, вес случайной рыбки отклоняется от веса средней рыбки на 30,4 г. Стандартное отклонение (SD) равно 30,4 г.

И здесь, мы бы уточнили свое первоначальное утверждение:

— В нашем пруду водятся золотые рыбки. Их средний размер (вес) равен 96,70 г, SD=30,4 г.

Теперь случайный рыбак не просто идет ловить рыбок весом 96,7 г, а отдает себе отчет в том, что, в среднем, вес выловленных рыбок будет на 30,4 г больше или меньше среднего веса. Наш рыбак теперь морально готов к тому, что ему может попасться как маленькая, так и большая рыбка.

А, если наш рыбак еще и математик, то он прикинет, что, предполагая, что вес рыбок подчиняется закону нормального распределения (а огромное число вещей и явлений в природе и мире распределены нормально), он будет ожидать, что 68% выловленных рыбок будет иметь вес плюс-минус 30,4 г от среднего 96,7 г, или от 66,3 г до 127,1 г.

И, если наш рыбак-математик с первой попытки поймает рыбку весом, например, 146,7 г (что будет отличаться от среднего веса на 50,0 г, или 1,645SD), он будет знать, что так везет лишь одному рыбаку из двадцати, потому что лишь 5% рыбок в пруду имеют вес более 146,7 г, согласно закону нормального распределения.

Единственная проблема заключается в том, что далеко не все в жизни сводится к примеру с рыбками, или к нормальному распределению. Так как речь может идти о генеральных совокупностях, распределенных не нормально, а как-то иначе.

И тут нам придется нырнуть, вслед за рыбками, к третьему, самому глубокому, уровню понимания.

3-й уровень понимания. Гистограмма распределения.

Чтобы понять, как распределена совокупность наших рыбок, лучше всего было бы «увидеть» всю картину в виде гистограммы распределения. Поскольку далеко не всегда мы будем иметь дело с нормальным распределением, одно лишь знание о размере стандартного отклонения и степени разброса значений в нашей выборке не даст нам полного понимания и осознания нашей совокупности.

Распределив имеющиеся 100 значений веса рыбок по диапазонам от 20 до 180 г с шагом в 20 г, мы бы увидели следующую картину:

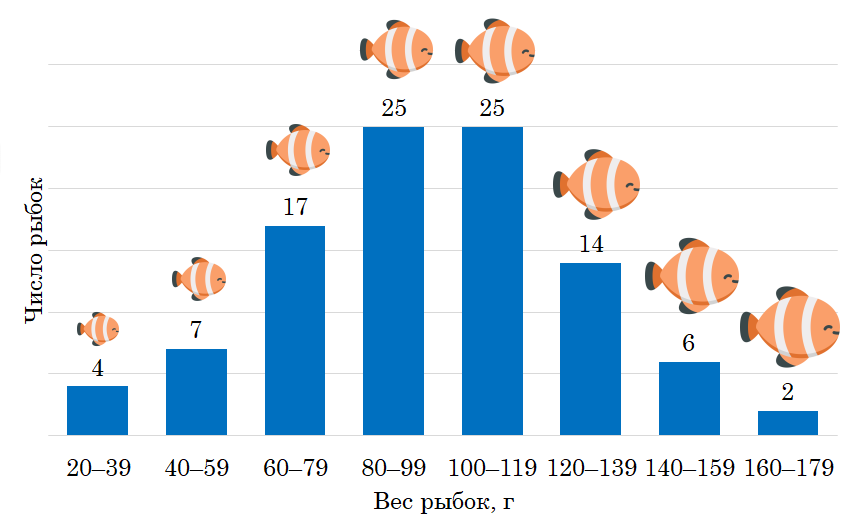
Только теперь мы получили полную картину того, какие рыбки плавают в нашем пруду. Мы словно разом прочувстовали, с чем имеем дело, увидели, насколько маловероятно выловить рыбку весом, например, больше 160 г, убедились, что вероятности встретить больших или маленьких рыбок одинаковы, а узнаваемая колоколообразная форма графика однозначно подсказала, что вес рыбок подчиняется нормальному распределению.

How much is the fish?

Мы идем на рыбалку, вооружившись полной картиной того, с чем имеем дело.

На первом уровне, уточнили средний вес рыбок.
На втором уровне, уточнили средний вес и его стандартное отклонение.
На третьем уровне, нарисовали гистограмму веса рыбок, чтобы разом увидеть портрет всех рыбок в пруду.

Крайне любопытная статья на сайте EvanMiller.org, «Ranking Items With Star Ratings», предлагает продвинутый способ расчета рейтингов, например, по пятибалльной шкале.

(Вообще, судя по интонации автора, история с рейтингами и методиками их расчета не так проста, как может показаться, и он неоднократно к ней возвращается.)

Из того, что удалось понять: во-первых, расчет среднего рейтинга не всегда позволяет однозначно определить место объекта относительно остальных объектов — например, средние рейтинги могут, банально, совпадать. Во-вторых, средний рейтинг не учитывает количество голосов, ведь по идее, чем больше голосов участвует в расчете рейтинга, тем надежнее этот рейтинг.

Простой пример — оценки двух сотрудников:

Осипов — 5, 5, 5, 5, 5, 2, 2, 2, 2, 2. Среднее = 3,50.
Сухонцев — 4, 4, 3, 3. Среднее = 3,50.

Неразрешимая, на первый взгляд, ситуация решается методами байесовской статистики (что бы конкретно это здесь ни значило), вуаля:

Осипов — 2,72.
Сухонцев — 2,63.

Чудесным образом то ли меньшее среднеквадратичное отклонение (0,58 против 1,58), то ли меньшее количество оценок (4 против 10), то ли все они вместе уточнили средний рейтинг Сухонцева, отдав ему предпочтение в несколько сотых.

Формула продвинутого расчета среднего рейтинга

Приготовьтесь, будет немного больно.

Итак, предполагается, что у нас есть K возможных оценок, считаемых по k, каждая оценка стоит s_k баллов («1» — это 1 балл, «2» — это 2 балла и т. д.). Имея N полученных оценок для каждого объекта, по n_k оценок для каждого k, можно посчитать рейтинг каждого объекта по формуле:

Где z_α/2 это 1−α/2 квантиль нормального распределения. Посчитанный рейтинг является нижней границей нормальной аппроксимации байесова доверительного интервала для среднего рейтинга. Принимая, например, α=0,10 (z=1,65), рассчитанный рейтинг S будет означать, что в 95% случаев средний рейтинг объекта будет выше S.

Упрощая, «продвинутый» расчет среднего рейтинга позволяет дать прогноз возможной средней оценки, рассчитываемой традиционным путем. Ну и, следовательно, как показано выше, ранжировать объекты даже при формально одинаковой средней оценке.

Пример расчета продвинутого среднего рейтинга

Вооружившись 2000 оценок по пятибалльной шкале условных территориальных офисов продаж, я посчитал средний рейтинг каждого офиса обычным и «продвинутым» способом.

Среднее 1.0 — средний рейтинг обычный, Среднее 2.0 — средний рейтинг продвинутый.

«Таганский» упал со 2-го на 4-е место по всей видимости, из-за того, что выборка в 66 оценок не дает достаточной уверенности в том, что его средний рейтинг действительно настолько высок, и в 90% случаев его рейтинг прогнозируется выше всего лишь 4,55, что примерно соответствует 4-му месту.

«Академический» формально был на 13-м месте, но, благодаря надежным 249 оценкам, для него прогнозируется, в 90% случаев, средний рейтинг не ниже 4,4, что поднимает его до 10-го места.

У меня сложилось ощущение, что формула более убедительно работает для коротких шкал оценок, как «от 1 до 5» в приведенном примере.

В любом случае, делюсь файлом в Google Таблицах — по идее, он считает рейтинги для всех шкал «длиной» до 100 оценок включительно, позволяет импортировать до 10 000 строк с оценками и корректировать уровень достоверности (90% в нашем примере).

Cм. также

https://www.evanmiller.org/ranking-items-with-star-ratings.html

Продвинутый способ расчета рейтинга в Google Таблицах

Недавно слушал «Вести ФМ», где обсуждались итоги единого дня голосования 8 сентября.

Меня заинтересовала следующая реплика ведущего, с 01:45:05:

Кстати, вот, слушатели из того же Хабаровского края пишут и, примерно, по количеству смсок делятся «50 на 50». 50% считают, что они позитивный выбор совершили, а 50% считают, что стало хуже, и это был негативный выбор. Это, понятно, не социологическое исследование. Ну, вот, просто я вижу десяток, восемь, где-то, смсок, и они примерно пополам делятся. Тоже любопытно.

К чести ведущего, абсолютно корректное замечание-«дисклеймер», что это не «социологическое исследование». И все же, что можно сказать о том, как, в реальности, делятся голоса, если у вас в наличии только 4 смски «за» и 4 смски «против»? Насколько соотношение «50 на 50», полученное на выборке в 8 смсок, подтверждает ровно то же самое распределение голосов в генеральной совокупности?

Считаем в Гугл Таблицах

Быстро воспроизводим эксперимент в Гугл Таблицах:

Итак, в тот день 4 человека прислали смски «за», 4 человека прислали смски «против». Логично предположить, что день на день не приходится, и сегодня это были одни слушатели, завтра смски будут присылать другие слушатели, и соотношение сил может быть «3 к 5», «5 к 3», «2 к 6» или «7 к 1» — любое сочетание теоретически возможно. Однако, если мы предполагаем, что взгляды аудитории делятся поровну, то чуть более вероятны сценарии «4 к 4», «3 к 5» или «5 к 3», а сценарии «8 к 0» или «1 к 7», например, менее вероятны.

Технически, мы имеем дело с биномиальным распределением — из 8 смсок мы ожидаем получить 4 смски «за», но не знаем наверняка, сколько их будет. Вероятность получить смску «за» равна 50% (допустим, что ровно 50% аудитории — «за»), в этом случае стандартная ошибка (SD, или σ) биномиального распределения рассчитывалась бы по формуле:

где p = 50%, а n = 8.

Считаем:

Получается, если вероятность получить смску «за» равняется 50%, то стандартное отклонение при выборке в 8 смсок равняется 17,68%!

Что же это означает на практике?

Это означает, что, поскольку имеющаяся выборка (8 смсок) крайне мала, доля случайности в нашем результате «4 „за“, 4 „против“», наоборот, крайне велика, и мы не можем уверенно говорить о строгом распределении голосов «50 на 50» среди всей аудитории «Вести ФМ». Единственное, что мы можем утверждать более-менее точно, это то, что истинная доля голосов «за» лежит в некотором интервале вокруг 50%. И величина этого интервала будет тем шире, чем больше мы захотим быть уверены в его надежности.

Предположим, мы хотим быть уверены в нашем доверительном интервале на 90%. (Оставляем себе право на ошибку в 10% случаев, другими словами). Согласно законам нормального распределения (а биномиальное распределение — это частный случай нормального), данный интервал определяется как 50%±1,645SD.

Такое несложно рассчитать в Гугл Таблицах:

Получается, что истинная доля голосов «за» лежит в интервале 50%±29,08%, т. е. от 20,92% до 79,08%. Примерно вот так это выглядит:

Значит, мы и близко не можем говорить о том, что «слушатели ... примерно ... делятся 50 на 50»! В лучшем случае (даже оставляя 10% на то, что мы ошибемся), мы можем говорить лишь об интервале от 21% до 79%.

Уточнение расчетов

Однако, интервал p±1,645SD тоже является достаточно грубой оценкой. Существуют более сложные, и немного более точные, способы оценить границы интервалов.

Воспользовавшись калькулятором Wolfram Alpha, можно получить следующие границы интервала:

Ну а если хотим, хотя бы, 45-55% получить?

Вот еще интересно: на какого размера выборке, если голоса в ней по-прежнему делятся строго «50 на 50», мы сможем говорить о доверительном интервале, суженном хотя бы до 45-55%?

Рассчитать такое несложно. Если речь идет об интервале 50%±5%, (и мы продолжаем придерживаться уровня уверенности в результате, равном нашим любимым 90%), то 5% должны составлять 1,645 стандартных отклонений (SD). Отсюда, SD = 3,04%. По формуле стандартного отклонения:

откуда несложно найти n = 270,6. Получается, нужно 270-272 смски с распределением голосов строго пополам, чтобы говорить об интервале от 45% до 55% с уровнем уверенности 90%.

См. также

https://en.wikipedia.org/wiki/Binomial_proportion_confidence_interval
Калькулятор на WolframAlpha.com
https://cyberleninka.ru/article/n/doveritelnye-intervaly-dlya-chastot-i-doley.pdf
Cтатистическая достоверность для застройщиков