Нормальное распределение

График и данные в Google Таблицах

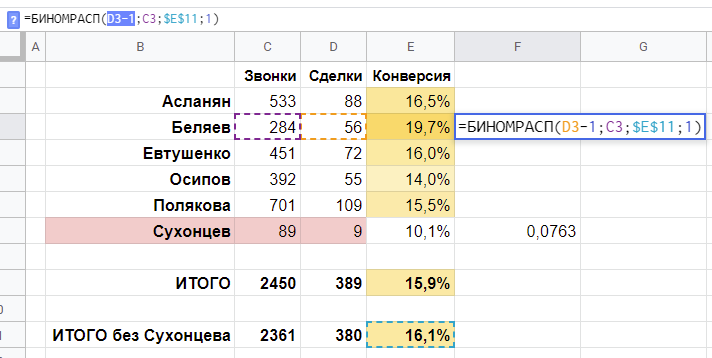
Любопытная особенность работы с понятием конверсия заключается в том, что, строго говоря, конверсия практически никогда не бывает определена точно.

Вот эти вот «конверсия звонка в продажу 18,4%», «CTR 3,1%», «конверсия в сделки 30%» — это всегда немного упрощенный подход, будто конверсия надежно измерена и, если и изменится, то мы это объясним объективными факторами, не допуская мысли, что изначально никаких «18,4%» и не было, а были только 38 договоров, которые мы сделали на 206 звонках, и это вовсе не значит, что их не могло бы быть больше или меньше.

Примерно, как местоположение электрона вокруг ядра атома не задается точными координатами, а лишь описывается некоторой областью, в которой он, наиболее вероятно, находится, наша конверсия — это тоже не конкретное число, а, в действительности, интервал, в котором она находится.

Расчет конверсии и когнитивное искажение

Рассмотрим вымышленный отдел продаж, в котором с этого года начали продавать новый продукт. Допустим, ммм, лимузины. Продукт не пользуется большим спросом, поэтому, пока что, данных для анализа не так много, или, лучше сказать, совсем мало:

Как видно из данных наших продаж, по итогам нескольких месяцев, мы имеем 4 сделки на 200 лидов (заявок), т. е. наша конверсия равна 4 / 200 = 2,0%

(Дополнительно, исходя из цифр пяти месяцев работы, мы можем примерно спрогнозировать 480 лидов на следующий год и, соответствнно, 480 * 0,02 = 9,6 сделок.)

В целом, на таких скудных данных ошибиться невозможно, поэтому, безусловно, такой прогноз не будет ошибочным. Однако, он содержит важное когнитивное искажение: 2,0% это не точное значение, а наиболее пока вероятное значение конверсии заявок в продажи наших лимузинов.

В действительности, конверсия не может быть определена точно. Она лежит в доверительном интервале от 0,4% до 3,6%. И в будущем году нужно прогнозировать не 9,6 сделок, а от 5 до 15 проданных лимузинов. К сожалению, определить этот диапазон точнее будет довольно самонадеянным.

Колокол конверсии

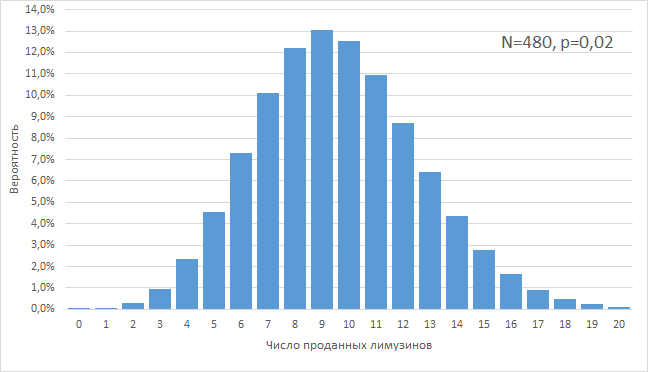
Исходя из предположения, что наша истинная конверсия стабильна, и точно равна 2,0%, мы можем прикинуть возможные варианты числа сделок на 480 лидов, ожидаемых в будущем году. Поскольку мы можем отвечать только за стабильность своей работы, но не можем учесть фактор случайности (настроение клиентов, форс мажор, случайная продажа другу гендиректора), всегда существует вероятность, что число сделок будет немного отличаться от прогнозируемых 480 * 0,02 = 9,6 сделок подобно тому, как число решек на 480 бросков монеты может немного отличаться от 240, и быть 235, 248, или, возможно, даже 223.

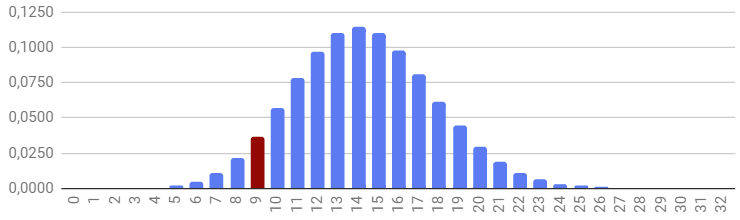
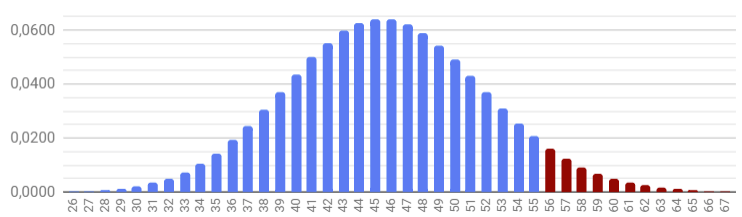
Графически это выглядит как колокол нормального распределения, где, чем дальше мы уходим от математического ожидания в 9 сделок в центре колокола, тем ниже становится вероятность сделать сильно меньше или сильно больше сделок:

Глядя на полученный график, приходится признать, что увидеть меньше 2-х и больше 19-ти сделок практически невероятно.

Но, можно ли сузить наш доверительный интервал?

Доверительный интервал конверсии

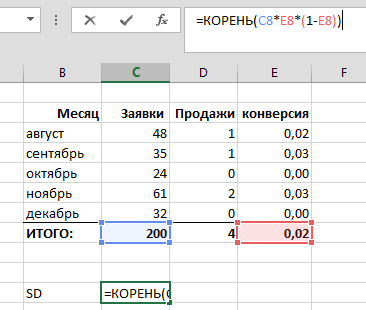
Стандартная ошибка (SD) для биномиального распределения считается по формуле:

где n — это число испытаний, p — вероятность успеха.

Для наших 200 заявок текущего года имеем:

SD = 1,98 сделок. Иными словами, согласно законам нормального распределения (а биномиальное распределение — это частный случай нормального распределения), примерно в 68% случаев, работая с истинной конверсией 2,0%, мы бы попали в доверительный интервал от 2,02 до 5,98 сделок, то есть +/-1SD.

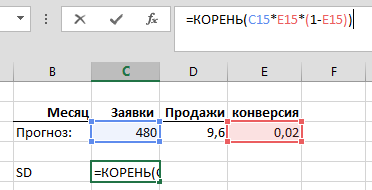
Для прогнозируемых 480 заявок будущего года получим:

SD = 3,07 сделок. По законам биномиального (нормального) распределения, известно, что в 68% случаев продажи будущего года будут лежать в пределах +/- 1SD от математического ожидания в 9,6 сделок, а в 90% случаев — в пределах +/- 1,645SD от матожидания. 3,07 сделок * 1,645 = 5,05 сделок, иными словами, в 90% случаев, работай мы весь следующий год с конверсией 2%, мы не выйдем за границы доверительного интервала «от 4,55 до 14,65 сделок». (Примечательно, что, обратно, в 1 случае из 10, мы, все-таки, выйдем за эти границы, по-прежнему, при этом, работая с «истинной» конверсией 2%.)

Любопытно, какой шум поднимет коммерческий директор, если по итогам года мы продадим всего 4 лимузина на 480 заявок, формально показав конверсию 0,83%... и еще более любопытно, что, статистически, это происходит в 1 из 27 отделов продаж. В одном из 27-ми случаев вас увольняют за невыполнение плана продаж, хотя вы по-прежнему работаете с «истинной» конверсией 2%.

Три конверсии на границе доверительного интервала

Как же тогда относится к результатам текущего года, где мы получили 4 сделки на 200 заявок?

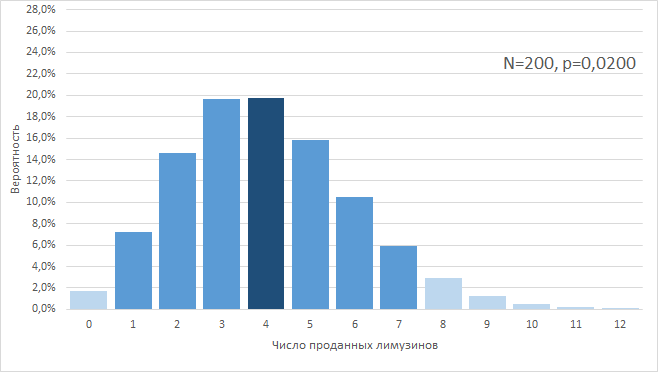
Первый случай, «2,00%». Его мы рассмотрели сразу. 4 / 200 = 0,02, т. е. наша конверсия равна 2%. При этом, по законам биномиального распределения, все равно есть вероятность колебаться в 90%-м доверительном интервале «+/-1,645SD», т. е., в интервале от 0,74 до 7,26 сделок на 200 заявок.

Выглядит это примерно так:

Наш результат в 4 сделки совпал с математическим ожиданием от конверсии 2,0%, хотя, в общем, он мог и не совпасть, в целом находясь в 90% доверительном интервале от 1 до 7 сделок.

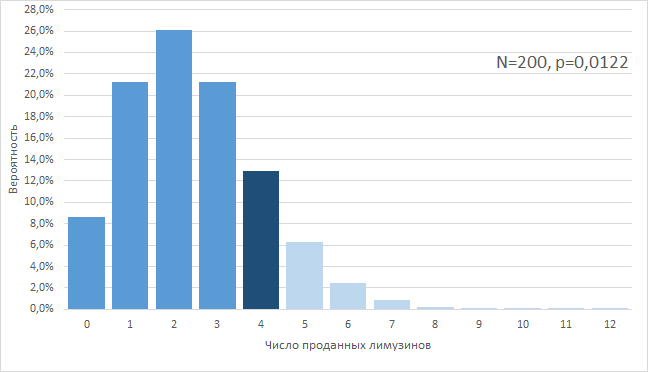
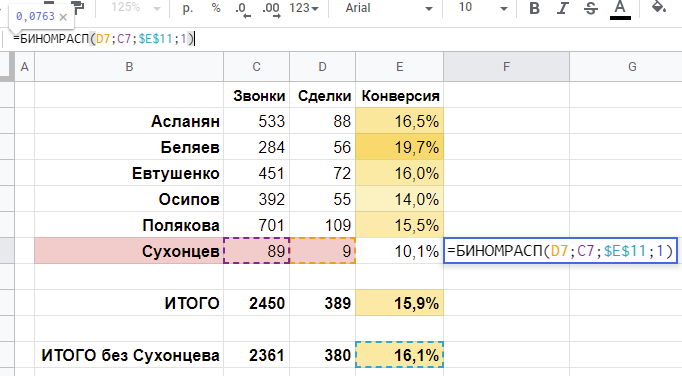
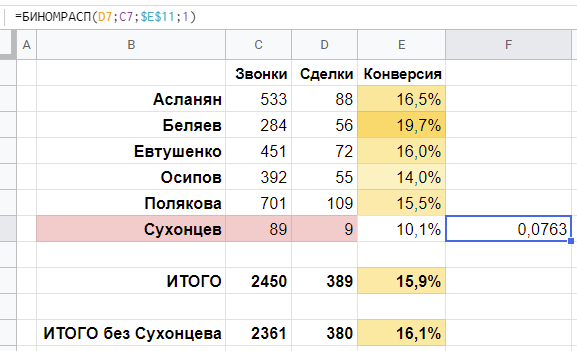
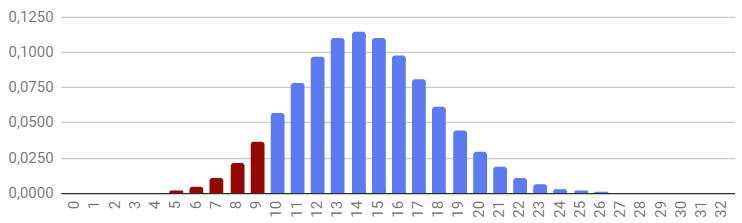
Второй случай, «1,22%». В этом случае, в реальности, наша «истинная» конверсия, на самом деле, ниже, и равна, например, 1,22%. Тогда матожидание числа проданных лимузинов примерно равно 2, и нам повезло сделать 4 продажи. Степень нашего везения такова, что сделать более 4 продаж мы могли бы только в 10% случаев. Т. е., мы остаемся в поле 90%-й вероятности, хотя и находимся на границе этого поля. Еще чуть-чуть, и нам повезет слишком сильно, а пока что нам везет «в пределах разумного»:

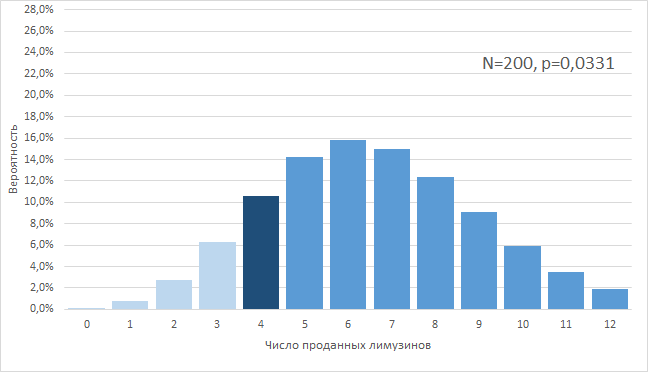
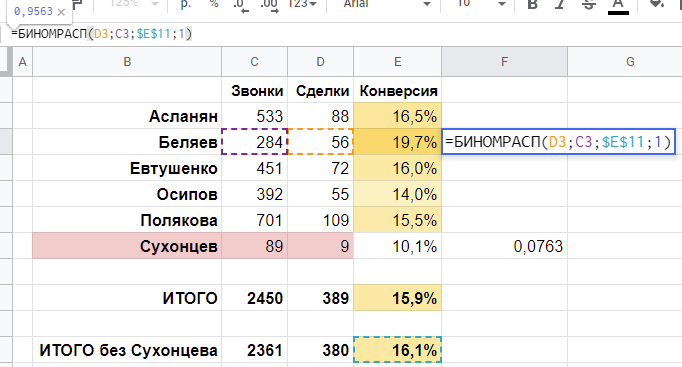
Третий случай, «3,31%». Теперь мы предположим, что в текущем году нам не везло, хотя весь год наша истинная конверсия была выше 2,0% и равнялась 3,31%. Матожидание для 200 заявок тогда равнялось бы примерно 6 проданным лимузинам, а сделать менее 4-х продаж было бы возможно лишь в 10% случаев. Тогда мы тоже остаемся в поле 90%-й вероятности, но находимся на левой границе этого поля с нашими невезучими 4 сделками.

Таким образом, приходится признать: мы не знаем наверняка, какая из 3-х конверсий — истинная. Нам привычно думать, что речь идет о 1-м случае, и мы делим 4 сделки на 200 заявок, получая конверсию 2,00%. Но никто не знает наверняка, является ли текущий год обычным или необычным, везло ли нам в нем, или не везло. В 90% случаев речь могла идти как о везении, и мы работали в действительности с конверсией 1,22%, так и о невезении, когда мы работали с конверсией 3,31%. Во всех 3-х случаях вероятность сделать 4 сделки на 200 заявок не выходила за границы 90%.

К сожалению, у нас пока слишком мало данных, чтобы утверждать что-то можно было более точно.

Нужно больше данных

Логично задать вопрос — а сколько нужно накопить данных, чтобы более-менее надежно говорить о конверсии 2,0%? Попробуем постепенно увеличивать размер выборки (число заявок, и, следовательно, продаж), пока не увидим, как 90%-й доверительный интервал сомкнется вокруг значения конверсии в 2,00%:

Надо ли говорить, что получить более нескольких десятков тысяч заявок-лидов может мало какой из отделов продаж. Поэтому, приходится признать, что ставить планы продаж и принимать кадровые решения относительно сотрудников, работающих с уровнями конверсии 1-5% — это безумие, и на таких маленьких числах математика в продажах не работает.

См. также:

http://italylov.ru/blog/all/ctatisticheskaya-dostovernost-koltrekinga/

Проблему, которую помогает решить использование матстатистики, я бы обозначил как «Повысить нельзя уволить» — вот перед нами результаты работы нашего отдела продаж, и назревают вопросы по нашему новому менеджеру Сухонцеву.

У сотрудника подходит к концу испытательный срок, план по сделкам ему был выставлен как «16 сделок на 100 звонков», поскольку исторически коммерческий директор видел конверсию звонков в сделки на уровне 16,1%.

Сухонцев, хорошо зарекомендовав себя за прошедшие 2,5 месяца работы, имеет 89 звонков и всего 9 сделок, что дает конверсию 10,1%.

«Увольнять,» — решает коммерческий директор.

Внимание, вопрос: справедливо ли решение коммерческого директора? Достаточно ли прошло времени (накоплено данных), чтобы принимать такое кадровое решение? Учтен ли фактор «невезения», и не может ли быть так, что Сухонцев работает не хуже остальных менеджеров, имея, в действительности, конверсию порядка требуемых 16%, но стабильно сталкиваясь с форс-мажорами у клиентов (5 клиентов «отвалились»), «черной полосой» в своей жизни и неудачно вставшей Луной в третьем доме Тельца?

Бросаем игральные кости

Вспоминая пример с бросками монетки, для разнообразия, в этот раз будем бросать игральную кость с 6-ю гранями. Вероятность выкинуть «1» составляет 1/6, или примерно 16,7%.

Математическое ожидание для 89 бросков игральной кости составляет 89 * 1/6 = 14,8 «единичек» (и по столько же «двоек», «троек» и т. д.), но, очевидно, их может быть не только 14-15, но и 12, 17, или, даже, 20. А вот совсем их не быть практически не может (хотя, теоретически, вероятность этого не нулевая).

Работу Сухонцева можно представить как броски игральной кости, где требуемый результат — «единичка»-сделка — выпадает примерно на каждый шестой бросок. Примерно, потому что исторически наблюдаемся конверсия в сделки составляет (без учета работы Сухонцева) 380 сделок на 2361 звонков, или 380/2361 = 16,1%. Математическое ожидание от его 89 «бросков» (звонков) составляет 89 * 0,161 = 14,3 «единичек» (сделок), но, интуитивно понятно, что их может быть чуть больше или чуть меньше.

Если рассчитать (позже узнаем, как) точные вероятности «выпадения» определенного числа сделок на 89 звонков и вывести их на графике, то наиболее вероятное событие («математическое ожидание») в 14 сделок окажется в середине графика, остальные возможные варианты (13 и 15 сделок, 12 и 16 сделок, и т. п.) каждый раз становятся все менее и менее вероятны, из-за чего график приобретает форму колокола:

Сказать, что результат в 9 сделок совсем невероятен не получается — какой-никакой, но этот столбик тоже заметен, и даже имеет вероятность в 0,037. Т. е., в 1 случае из 27 он случается, что, может, и маловероятно, но не крайне маловероятно.

Осталось разобраться, как мы получили вероятность «в 1 случае из 27», и как это связать с кадровыми решениями в отделе продаж.

Считаем биномиальное распределение

И в Excel, и в Google Таблицах есть встроенная функция биномиального распределения. Она-то и даст нам ответ на вопрос, пора ли увольнять невезучего Сухонцева.

В ячейке напротив его конверсии в 10,1% посчитаем функцию:

=БИНОМРАСП(D7;C7;$E$11;1)

В данной функции указываем по порядку: значение числа успехов (сделок), значение числа попыток (звонков), значение вероятности успеха (конверсия 16,1%). Последний, 4-й параметр, указываем «1».

Что за 0,0763 мы получили? 0,0763 — это вероятность получить не более 9 сделок на 89 звонков при вероятности сделки 16,1%. Таким образом, это вероятность получить от 0 до 9 сделок включительно при данных параметрах. Обратно, 1-0,0763 = 0,9237 — это вероятность получить 10 и более сделок.

(Кстати, если 4-й параметр в функции поменять на «0», мы получим вероятность получить ровно 9 сделок).

Можно сказать, что, принимая сумму всех столбиков на графике за 1, сумма столбиков «0»-«9» равна 0,0763, или 7,63%. Как видим, гораздо более вероятно попасть в синюю часть колокола нормального распределения, чем в красную (92,37% против 7,63%).

Вывод: вероятность Сухонцеву, работая в действительности с конверсией 16,1%, случайно (возможна «черная полоса», помните?) получить не более 9 сделок из 89 звонков, равна 7,63%. Обратно, 92,37% вероятность того, что Сухонцев получил бы 10 и более сделок. Грубо говоря, 7,63% за то, что ему не повезло, а 92,37% за то, что одним невезением тут не обошлось, и, скорее всего, он работает с конверсией ниже 16,1%.

Таким образом, если для коммерческого директора уровня 90% уверенности достаточно, то Сухонцева можно увольнять с испытательного срока — менеджер, действительно, не выполняет план. Если же нужен уровень 95% уверенности, то данных пока недостаточно, и желательно понаблюдать чуть дальше.

Какой же уровень уверенности выбрать? Правильного ответа здесь не существует.

Если его выбрать слишком низким, то мы можем случайно уволить хороших менеджеров, зато не придется терять сделки, продолжая работать с плохими.

Если выбрать его слишком высоким, то слишком долго придется копить данные для принятия математически обоснованного решения об увольнении плохого менеджера, зато и меньше вероятность случайно уволить хорошего. По моему мнению, уровень 90% для описанного кейса оптимален. Сухонцева можно увольнять.

Постойте, а что с 19,7% Беляева?

Действительно, если существуют «плохие» менеджеры, для которых с вероятностью 92,37% конверсия ниже требуемых 16,1%, то, логично, могут существовать и «хорошие».

Наше внимание обратили на себя 19,7% конверсии Беляева. За полгода работы он сделал 56 сделок на 284 звонка, при прогнозируемых 0,161*284 = 46 сделках. Могло ли ему везти эти полгода? Могло ли быть так, что, работая в действительности как все, с конверсией 16,1%, он случайно получил больше сделок, чем прогнозировал коммерческий директор?

Функция биномиального распределения дает результат в 0,9563 — то есть, с вероятностью 95,63%, работая как все, он бы получил не более 56 сделок... но он и не сделал более 56 сделок! Он сделал ровно 56!

Доработаем функцию, пересчитав ее для 56-1 = 55 сделок:

Для 55 сделок результат получился 0,9402. То есть, с вероятностью 94,02% Беляев (работая с конверсией 16,1%) получил бы не более 55 сделок. Получается, вероятность получить более 55 сделок равна оставшимся 5,98%! Получается, наш Беляев попал в кусочек своего колокола распределения, только с другого конца, и вероятность попасть туда составляет всего около 6%.

Коммерческий директор уже решил, что, прежде чем принимать кадровые решения, он хочет быть уверен в результатах на 90%. Но в результатах Беляева он уверен на 94,02%! Значит, остается всего 5,98% на то, что Беляеву повезло.

Значит, либо ему так повезло, хотя он, в действительности, работает как все (с конверсией 16,1%) и недостоин большей зарплаты, либо, он работает с конверсией выше 16,1% и будет справедливо вознаградить его.

6% явно проигрывают 94%, поэтому, Беляев получает повышение.