Переписываясь на днях с коллегой в Телеграме, в очередной раз увидел примерно вот такой отчет (сейчас просто нарисовал похожий) — сверху недели, сбоку, допустим, территориальные офисы продаж (там были месяцы и продажи по типам продукта, но для целей этой заметки это совершенно не имеет значения):

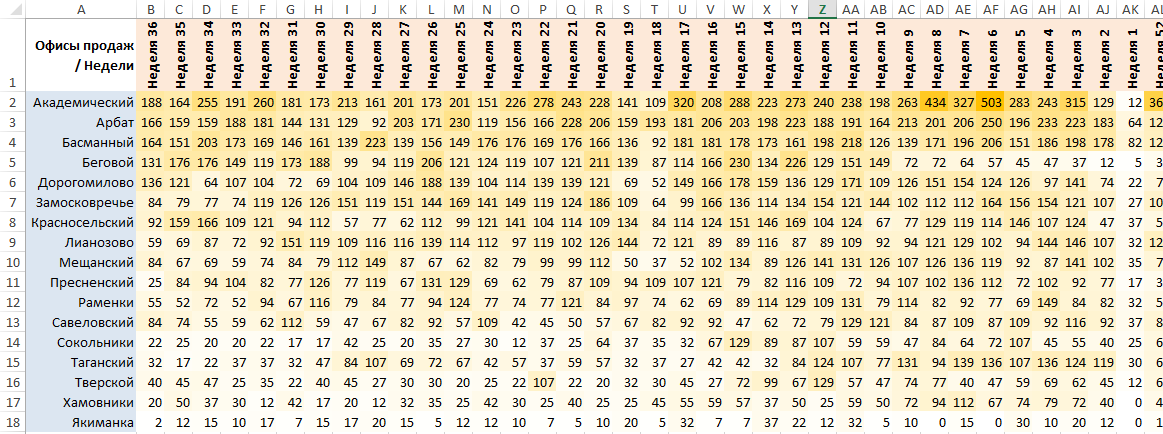
Воспользовавшись «Условным форматированием» в Экселе, замечаем, что на 6-й неделе в офисе «Академический» было 503 продажи. В общем, до этого момента ничего необычного, и так выжали 90% из данных, можно работать с отчетом и анализировать, что душе угодно.

Однако, есть несложная доработка, позволяющая выжать из данных еще лишние 5%.

Что, собственно, ищем

На картинке особо не видно, но чем ниже по списку, тем меньше в среднем продаж в каждом следующем офисе. То есть, будем считать, что офисы продаж все очень разные, и некорректно сравнивать «Академический» с «Якиманкой» — нехитрым вычислением получается, что «Академический» в среднем делал 242 продажи в неделю, а «Якиманка» — всего 13. Предположим, что тому есть объективные причины, и никто и не требовал от всех офисов показывать одинаковые результаты.

И тогда можно задать себе вопрос: достаточно ли просто анализировать абсолютные показатели по нашим офисам? И не будет ли правильнее копнуть вглубь, и попробовать найти такие показатели, которые выбиваются из общей картины? Такие недели, которые были аномальными для данного офиса продаж.

Здесь и далее под «аномалией» я буду понимать такое значение продаж, которое слишком отличается от среднего по данном офису. Как в большую (и надо разобраться, как повторить этот результат) или в меньшую (проанализировать, как избежать неудачи в будущем) сторону.

Распределяем результаты офиса «Академический»

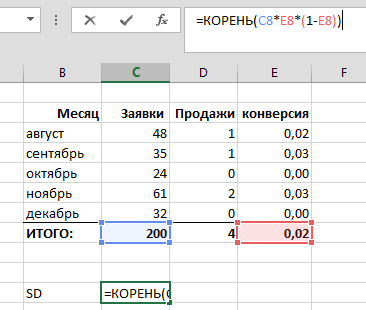
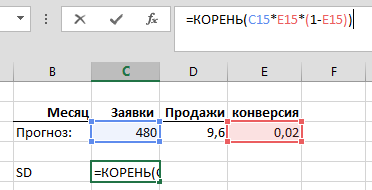
Изучив результаты продаж офиса «Академический» за прошедшие 43 недели, мы рассчитали, что в среднем они делают 241,5 продаж в неделю, при этом стандартное отклонение (SD) равно 86,3.

Напомню формулы:

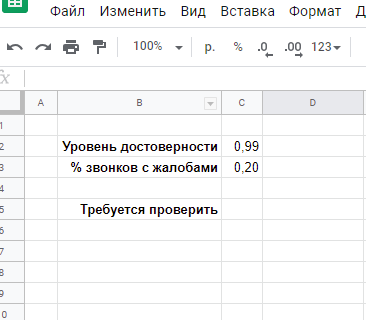
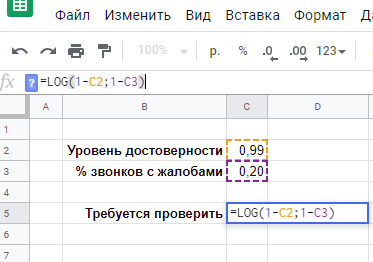
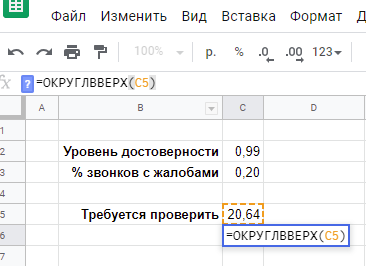
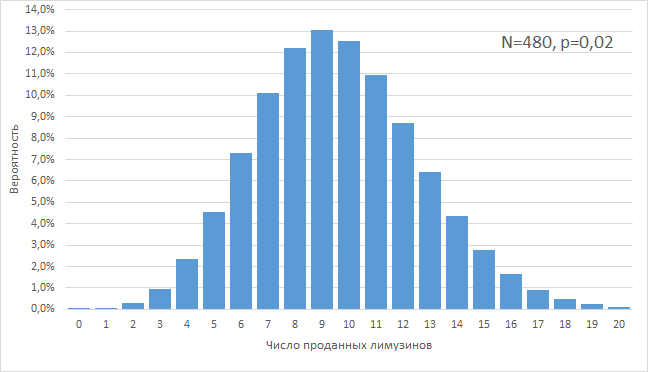
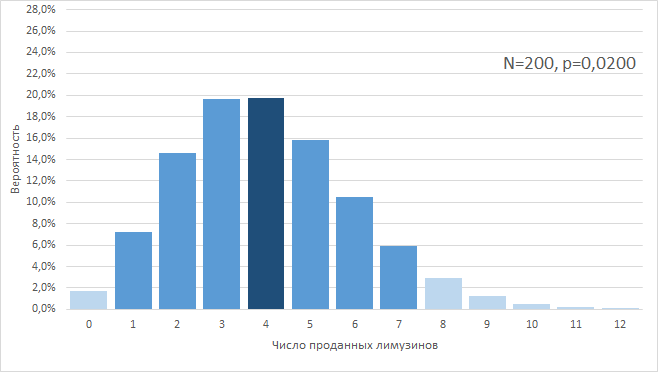
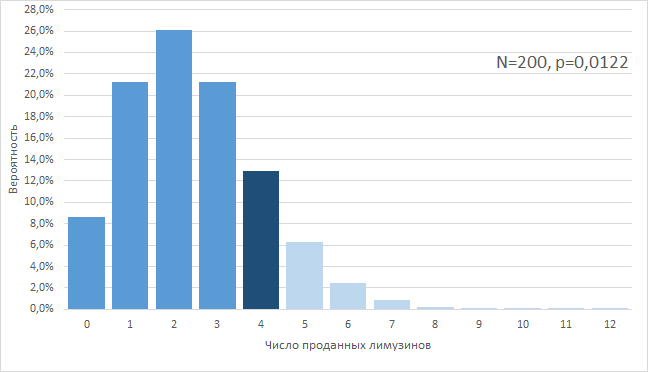
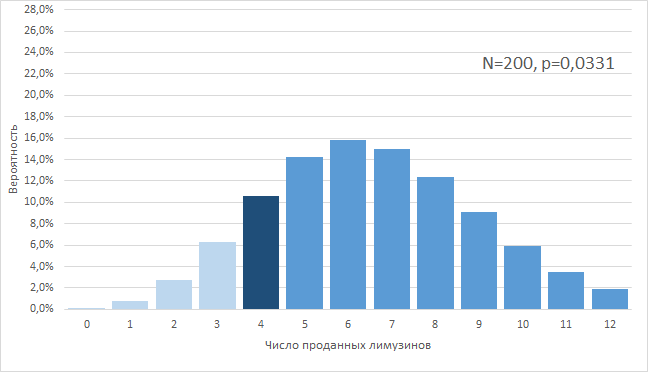
=СРЗНАЧ(B2:AR2)

=СТАНДОТКЛОН.В(B2:AR2)

Можно, гипотетически, представить, что мы имеем возможность наблюдать за результатами офиса «Академический» 200 (sic!) лет, при условии, что все это время среднее и стандартное отклонение не меняются, т. е., грубо говоря, они работают, как работали. В этом случае, мы увидели бы распределение результатов продаж, близкое к нормальному:

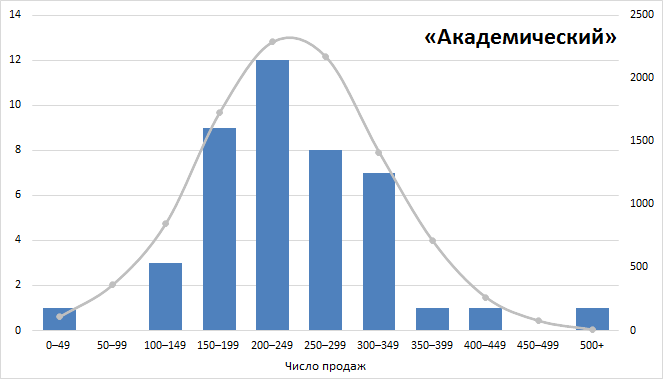
Давайте даже еще раз перерисуем картинку. 2 290 недель из 10 000 они бы делали от 200 до 249 продаж в неделю:

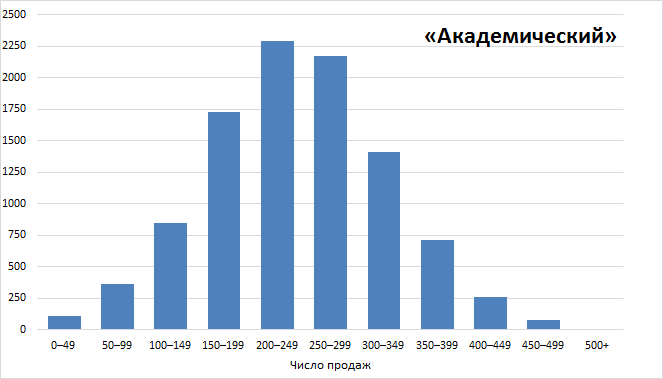
Понимаете, к чему я клоню?

Если только допустить, что результаты продаж подчиняются законам нормального распределения (грубо говоря, равновероятно продать как чуть больше, так и чуть меньше среднего), существует некоторое разумное отклонение от среднего, в пределах которого было бы глупо всерьез говорить о «спаде продаж» или «невероятном успехе». Иными словами, бессмысленно считать «аномалией» то, что лежит в пределах разумного отклонения от среднего.

Остается сформулировать критерии «разумности» и научить отчет сигнализировать об «аномалиях».

Вспоминаем теорию

Если вкратце, то, допустив на минутку, что мы имеем дело с нормальным распределением, вычислив среднее значение и стандартное отклонение (SD), мы можем уверенно говорить о том, что 90% данных в отчете не будут выходить за границы ±1,645SD от среднего.

Применительно к офису «Академический» речь идет о том, что для 90% времени результаты их продаж будут лежать в диапазоне от 100 до 383, или 241,5±142,0. Поэтому до тех пор, пока цифры не вышли за пределы этих границ, мы не наблюдаем ничего необычного.

Сразу оговоримся: конечно, степень «необычности», или «аномалии», каждый определяет для себя сам. Для одних, подозрение могут вызывать показатели, выбивающиеся за рамки 80%-ной вероятности (±1,28SD), для других — терпимым будет отклонение в ±1,96SD, что соответствует 95%-й вероятности. Тогда, первые будут бить искать причины «аномалии» в 20% случаев, вторые — в 5%. Каждую пятую неделю но отчете у коммерческого директора первые будут объяснять, что произошло, и почему, тогда как вторые будут делать это раз в 4-5 месяцев.

Допущение о том, что продажи в территориальных офисах, число посетителей на сайте, количество рекламных звонков, клики по баннеру распределяются по закону нормального распределения, дало нам потрясающую возможность оценивать вероятность наступления «аномалии» — слишком сильного отклонения от среднего значения. Обратно, оно учит нас не бить тревогу там, где отклонение, хотя и есть, не является достаточно сильным, и делает, отчасти, бессмысленным анализ и разбор ситуаций, когда показатель отклоняется в пределах разумного.

Перекрашиваем отчет, включаем зеленые и красные «лампочки»

Теперь мы хотим переделать отчет о продажах в территориальных офисах таким образом, чтобы напротив подозрительно больших или подозрительно маленьких значений загорались бы зеленые и красные «лампочки».

Нам необходимо научить отчет «включать» наши «лампочки», если значение в ячейке становится больше или меньше границ 90%-го диапазона, т. е. в примерно 90% случаев ни одна из «лампочек» «загораться» не будет, в примерно 5% случаев будет «загораться» красная «лампочка», и еще в примерно 5% — зеленая.

Применительно к «Академическому», мы хотим выделять красным значения, меньшие чем 241,5-1,645*86,3, т. е., меньшие, чем 100, и мы ходим выделять зеленым значения, большие, чем 241,5+1,645*86,3, т. е., большие, чем 383.

Нам остается рассчитать границы включения «лампочек» по каждому из офисов продаж, рассчитав последовательно: среднее значение продаж, стандартное отклонение (SD), нижнюю границу 90%-го диапазона, верхнюю границу 90%-го диапазона.

Используемые формулы:

=СРЗНАЧ(B2:AR2)

=СТАНДОТКЛОН.В(B2:AR2)

=B2-1,645*C2

=B2+1,645*C2

У нас получилась следующая таблица, содержащая расчеты по нижним и верхним границам того, что мы далее будем считать «аномалией»:

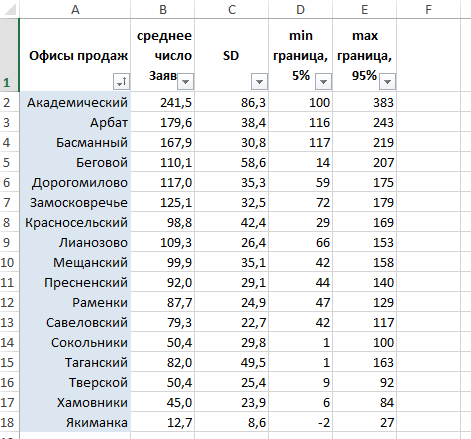
Теперь, используя инструмент «Условное форматирование» — «Правило выделения ячеек» — «Меньше...»/«Больше...», последовательно для каждого из 17-ти офисов продаж настраиваем правила подсветки ячеек красным и зеленым, в зависимости от того, будет ли значение ниже нижней границы 90%-го диапазона, или выше верхней границы:

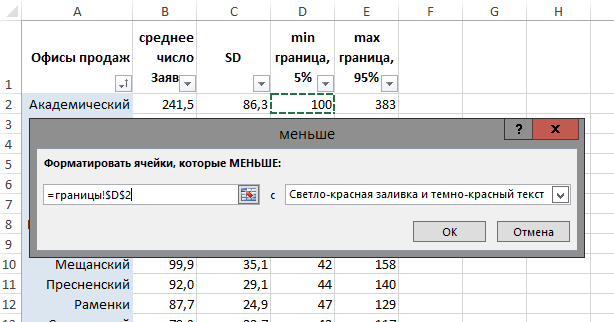
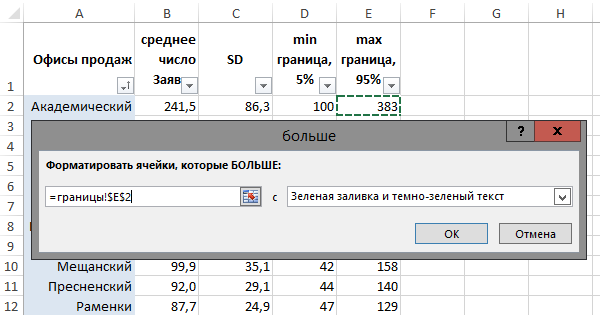
Дополнительно выставляем светло-серый цвет текста, чтобы подсвеченные «аномалии» были еще более заметны. Добавляем градиент от белого к светло-серому, чтобы сохранить первоначальную идею выделять большие значения более темной заливкой. Законченная таблица приобретает следующий вид:

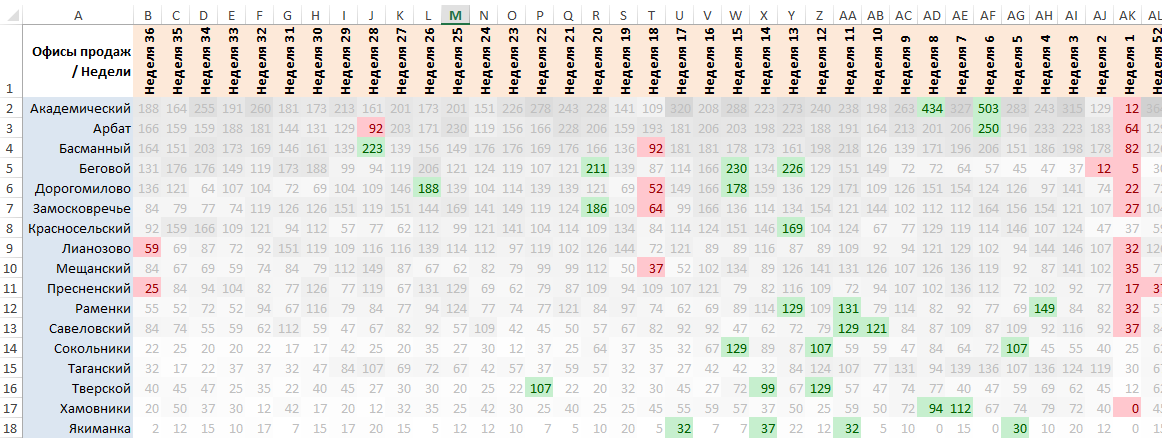
Выводы

Используя идею о разбросе значений вокруг среднего в нормальном распределении, нам удалось доработать наш отчет о территориальных офисах таким образом, что мы не просто видим результаты, но и теперь отдельно включаем красные и зеленые «лампочки» для тех результатов, которые представляют интерес, как «аномалии» — маловероятно маленькие или маловероятно большие значения, определив уровень «аномалии» как все, что выходит за пределы 90% вероятности.

На днях пришел в голову такой пример: предположим, подрядчик жалуется на плохую связь «в каждом пятом» звонке.

Наша задача проверить, справедлива ли гипотеза, что 20% звонков имеют проблемы со связью. Причем, как всегда, мы не просто сделаем 100 тестовых звонков (на это у нас нет ресурсов), а сформулируем нулевую гипотезу, альтернативную гипотезу, и проверим ее с заданным уровнем достоверности.

Выдвигаем гипотезу и определяем уровень достоверности

Нулевой гипотезой (H₀) пусть будет предположение, что со связью все в порядке, или, по крайней мере, проблемы встречаются реже, чем в 20% звонков.

Альтернативной гипотезой (H₁), которую мы будем проверять, пусть будет предположение подрядчика, что в каждом пятом звонке наблюдаются помехи. То есть, по крайней мере, в 20% звонков есть проблемы со связью.

Уровень достоверности — это наша уверенность в результатах эксперимента. Чем он выше, тем больше придется сделать проверочных звонков, поэтому мы заложим 1% на возможную ошибку, и выберем уровень достоверности в 99% (1%, что, если даже эксперимент не подтвердит проблем со связью, они, в действительности, могут быть).

Cобираем формулу для расчета выборки

Предположим, цель эксперимента — опровергнуть альтернативную гипотезу H₁ («есть проблемы»), подтвердив нулевую гипотезу H₀ («все в порядке»). Чтобы сделать это, нам будет достаточно продемонстрировать N подряд успешных звонков без признаков проблем со связью, при этом допуская вероятность, равную или меньше 1%, что нам просто повезет, и, при наличии, в действительности, проблем с оборудованием, они случайно не проявят себя ни в одном из N звонков.

Из предположения подрядчика вытекает, что 80% звонков не имеют проблем. Вероятность отсутствия сбоев в N звонках подряд равна 0,80^N. Нам нужно подобрать минимальное N, при котором вероятность упадет до 1%: 0,80^N = 1%

Получается, нам нужно вычислить логарифм 1% по основанию 80%!

Загружаем в Гугл Таблицы:

Формула для ячейки C5 будет выглядеть как

=LOG(1-C2;1-C3)

Нужно сделать 20,64 звонка. (Проверяем: 0,80^20,64 = 0,9995%, идеально.)

Остается только добавить округление:

=ОКРУГЛВВЕРХ(C5)

или сразу

=ОКРУГЛВВЕРХ(LOG(1-C2;1-C3))

Проверяем гипотезу

Если альтернативная гипотеза H₁ нашего подрядчика верна, и мы испытываем проблемы со связью в каждом пятом звонке, то, вероятность не заметить проблем в 21 тестовом звонке подряд составляет порядка 1%. Иными словами, либо это крайне редкое совпадение (1%), либо альтернативная гипотеза о проблемах в 20% звонков неверна (99%), и мы оставляем нулевую гипозеу H₀. С вероятностью 99% мы уверены, что проблем со связью не наблюдается.