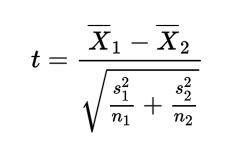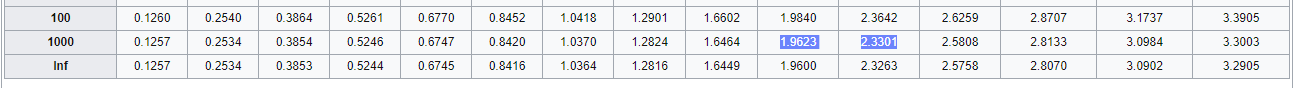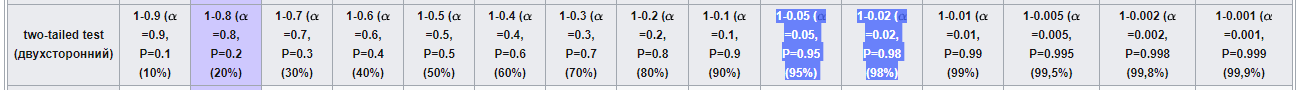На днях пришел в голову такой пример: предположим, подрядчик жалуется на плохую связь «в каждом пятом» звонке.

Наша задача проверить, справедлива ли гипотеза, что 20% звонков имеют проблемы со связью. Причем, как всегда, мы не просто сделаем 100 тестовых звонков (на это у нас нет ресурсов), а сформулируем нулевую гипотезу, альтернативную гипотезу, и проверим ее с заданным уровнем достоверности.

Выдвигаем гипотезу и определяем уровень достоверности

Нулевой гипотезой (H₀) пусть будет предположение, что со связью все в порядке, или, по крайней мере, проблемы встречаются реже, чем в 20% звонков.

Альтернативной гипотезой (H₁), которую мы будем проверять, пусть будет предположение подрядчика, что в каждом пятом звонке наблюдаются помехи. То есть, по крайней мере, в 20% звонков есть проблемы со связью.

Уровень достоверности — это наша уверенность в результатах эксперимента. Чем он выше, тем больше придется сделать проверочных звонков, поэтому мы заложим 1% на возможную ошибку, и выберем уровень достоверности в 99% (1%, что, если даже эксперимент не подтвердит проблем со связью, они, в действительности, могут быть).

Cобираем формулу для расчета выборки

Предположим, цель эксперимента — опровергнуть альтернативную гипотезу H₁ («есть проблемы»), подтвердив нулевую гипотезу H₀ («все в порядке»). Чтобы сделать это, нам будет достаточно продемонстрировать N подряд успешных звонков без признаков проблем со связью, при этом допуская вероятность, равную или меньше 1%, что нам просто повезет, и, при наличии, в действительности, проблем с оборудованием, они случайно не проявят себя ни в одном из N звонков.

Из предположения подрядчика вытекает, что 80% звонков не имеют проблем. Вероятность отсутствия сбоев в N звонках подряд равна 0,80^N. Нам нужно подобрать минимальное N, при котором вероятность упадет до 1%: 0,80^N = 1%

Получается, нам нужно вычислить логарифм 1% по основанию 80%!

Загружаем в Гугл Таблицы:

Формула для ячейки C5 будет выглядеть как

=LOG(1-C2;1-C3)

Нужно сделать 20,64 звонка. (Проверяем: 0,80^20,64 = 0,9995%, идеально.)

Остается только добавить округление:

=ОКРУГЛВВЕРХ(C5)

или сразу

=ОКРУГЛВВЕРХ(LOG(1-C2;1-C3))

Проверяем гипотезу

Если альтернативная гипотеза H₁ нашего подрядчика верна, и мы испытываем проблемы со связью в каждом пятом звонке, то, вероятность не заметить проблем в 21 тестовом звонке подряд составляет порядка 1%. Иными словами, либо это крайне редкое совпадение (1%), либо альтернативная гипотеза о проблемах в 20% звонков неверна (99%), и мы оставляем нулевую гипозеу H₀. С вероятностью 99% мы уверены, что проблем со связью не наблюдается.

Распространенным инструментом оценки качества работы менеджеров отдела продаж является аудит качества телефонных звонков, «прослушка».

Предположим, вы задались целью не просто замерить качество телефонных звонков, но зафиксировать рост этого качества. Например, провели обучение (тренинг) менеджеров, либо предложили новую мотивацию за соблюдение стандартов качества, либо что-то еще.

Логично предположить, что рост качества в первом попавшемся, после тренинга, звонке, не будет однозначно свидетельствовать о росте качества в остальных звонках. Скорее всего, и второй удачный звонок тоже однозначно не подтвердит гипотезу, что качество выросло.

Таким образом, речь будет идти о том, что вам придется прослушать если не все, то, по крайней мере, достаточное число звонков после введенных вами изменений, и число звонков, которые необходимо будет прослушать, на самом деле, можно однозначно рассчитать.

Считаем размер выборки

На 15-й странице работы «Планирование размеров выборки для исследований в бихевиоризме» мне попался подходящий пример 2.4 и формула для расчета таких выборок:

В данном примере рассматривается изменение оценки ACT-теста по математике с 24,5 (дисперсия 8,2) до 26,0 баллов при α = 0,05 и мощности = 0,90.

Для удобства работы, я собрал приведенную формулу в Гугл-таблицах:
Калькулятор размера выборки

Вам остается скопировать файл, и можете подставлять нужные вам значения. Достоверность разумно выбирать от 80% до 95%, значение мощности — от 60% до 80%. Указываете средний балл оценки звонков до изменений, стандартное отклонение (SD) оценки звонков «до», и ожидаемый средний балл оценки звонков после изменений.

Верификация полученных результатов

Важно понимать, что, даже прослушав требуемое количество звонков «после», все равно необходимо проверять наличие статистически значимых различий через калькулятор А/Б-тестов.

См. также:

https://habr.com/ru/post/339798/
https://people.ucsc.edu/~dgbonett/docs/wrkshp/LectureNotes.pdf

Если однажды перед вами оказывались два набора похожих данных, вам, вероятно, приходило в голову задаться вопросом: насколько эти данные различаются между собой? Или, что еще более важно, наблюдаются ли статистически значимые различия между этими выборками?

Поясню, о чем идет речь.

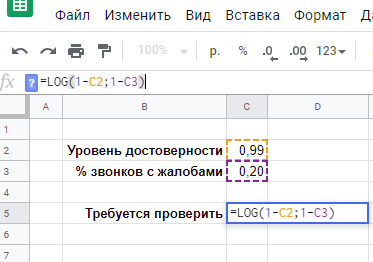
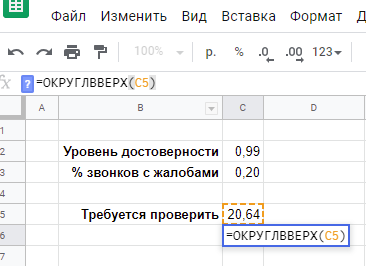
Допустим, вы проанализировали звонки за прошедший год и обратили внимание, что среднее время звонка в первой половине дня — 2 мин 45 сек, а во второй половине дня — 2 мин 57 сек. Следует ли из этого, что звонки после обеда в среднем длятся дольше? Или это простое совпадение, и, возьми вы звонки за год до этого, вы бы увидели другую картину?

Или, например, вы замеряли уровень гемоглобина у контрольной группы до начала исследований нового лекарства, и после. Предположим, средний уровень вырос с 142,5 г/л до 147,1 г/л. Достаточно ли опираться на увеличение среднего, чтобы сделать заключение об эффективности лекарства? Или, возможно, исследование нужно повторить? Увеличив размер контрольной группы, например?

Уже из постановки вопроса очевидно, что одной разницы между средними в двух выборках недостаточно, чтобы научно подтвердить их различие.

Вот почему мы обратимся к формуле расчета и таблице значений t-критериев Стьюдента, чтобы научиться делать математически корректные выводы о статистически значимых различиях между двумя выборками. Или, другими словами, научиться видеть разницу, когда она не заметна, или игнорировать ее, даже если кажется, что она есть.

Рассмотрим вопрос на примере.

Анализ длительности звонков Асланян и Евтушенко

В вашем отделе продаж работают 2 менеджера — Ольга Асланян и Кирилл Евтушенко. Вы получили данные по длительности их разговоров с покупателями и хотите проверить гипотезу, что разговоры Асланян в среднем длятся дольше разговоров Евтушенко.

Посчитаем среднюю длительность звонка, стандартное отклонение и число звонков, которые попали в выборке.

=СРЗНАЧ(B2:B999)

=СТАНДОТКЛОН(B2:B999)

=СЧЁТ(B2:B999)

В среднем, звонки Асланян длятся на 34,5 сек дольше звонков Евтушенко. (Кроме того, разброс длительности ее звонков больше, т. к. больше стандартное отклонение. Грубо говоря, короткие и длинные звонки у Асланян найти проще, чем у Евтушенко).

Достаточно ли полученных данных, чтобы сделать вывод о правильности гипотезы, что Асланян в среднем дольше общается с клиентами, чем Евтушенко? На самом деле, нет. Всегда существует вероятность, что в выборку Асланян случайно попали более длинные звонки, а в выборку Евтушенко — более короткие. Чем больше звонков доступно для анализа (а нам достались 242 и 209 звонков, что не так уж и мало), тем более надежен результат, но он никогда не надежен на 100%.

Впрочем, надежность 100% нам и не нужна. Не ракету к Марсу запускаем. Даже если нам удастся проверить нашу гипотезу с вероятностью 90-95%, этого будет вполне достаточно для большинства случаев. Пускай мы оставим себе шанс ошибиться в 5-10% случаев, зато нам не нужно будет ждать несколько лет, чтобы накопить достаточно данных для анализа, и управленческие решения (разбор звонков с менеджером, анализ продаж, корректировки скриптов) мы сможем принять уже сейчас.

Рассмотрим два способа, как нам проверить, случайность ли, что звонки Асланян в среднем длиннее звонков Евтушенко.

Проверка гипотезы о равенстве среднего. Простой способ

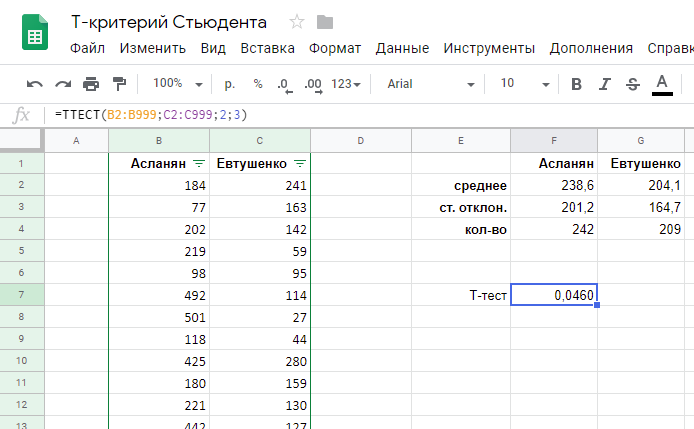
И в Google Таблицах, и в Microsoft Excel, есть функция ТТЕСТ. Воспользуемся ей для анализа наших выборок.

=ТТЕСТ(B2:B999;C2:C999;2;3)

У функции 4 атрибута, идущие через точку с запятой.

1. Диапазон ячеек, содержащих первую выборку.
2. Диапазон ячеек, содержащих вторую выборку.
3. Количество хвостов распределения. Выбираем «2», чтобы проверить наличие различий вообще, и «1», чтобы проверить, звонки Асланян длиннее, а не наоборот.
4. Тип применения t-критерия. По умолчанию выбираем «3». («2» выбираем если стандартные отклонения очень близки, «1» — если, например, вы сравниваете средний балл одних и тех же учеников на начало и конец года попарно.)

Итак, Т-тест дал вероятность 0,04595, или, округленно, 4,6%.

Что же это за вероятность? В нашем примере это вероятность того, что статистически значимые различия между звонками Асланян и Евтушенко отсутствуют. Технически, это вероятность, что наша «нулевая гипотеза» («нет разницы между выборками») была верна, а «альтернативная» («Асланян общается с покупателями дольше Евтушенко») — неверна.

Оставшиеся 95,4% составляют вероятность того, что между выборками есть статистические различия, и «альтернативная гипотеза» о различиях между выборками верна.

Вывод: с вероятностью 95,4% Асланян, действительно, в среднем общается с клиентами дольше Евтушенко. (С вероятностью 4,6% статистически значих различий между их звонками нет).

Проверка гипотезы о равенстве среднего. Сложный способ

Сложный способ будет состоит из двух этапов: расчет t-критерия Стьюдента и сравнение полученного значения t-критерия с контрольным.

На первом этапе рассчитаем t-критерий Стьюдента по следующей формуле:

X₁ и X₂ — средняя длина звонков в первой и второй выборке (238,6 сек и 204,1 сек)
s₁ и s₂ — стандартные отклонения первой и второй выборок в квадрате (их дисперсии, другими словами) (201,2² и 164,7² для наших выборок)
n₁ и n₂ — число звонков в первой и второй выборках (242 и 209 звонков)

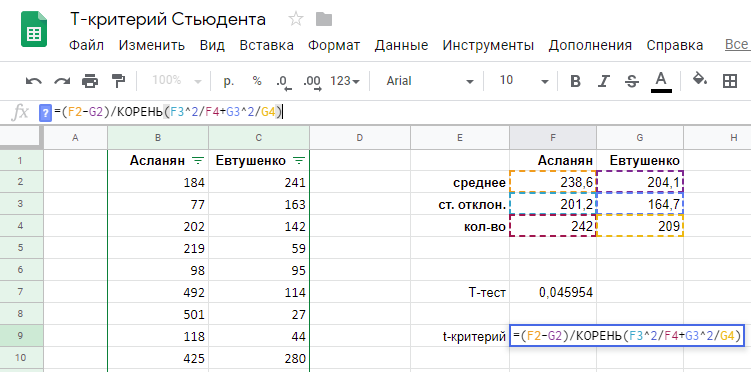
Воспользуемся листочком бумаги и калькулятором, или же посчитаем все прямо в Google Таблицах:

=(F2-G2)/КОРЕНЬ(F3^2/F4+G3^2/G4)

t-Критерий равен 2,0014.

Осталось разобраться, что делать с вычисленным значением нашего t-критерия.

Но перед этим посчитаем число степеней свободы по формуле n₁+n₂-2:

242 + 209 — 2 = 449 степеней свободы

Воспользуемся теперь таблицей коэффициентов Стьюдента из Википедии, найдя строку, соответствующую нашим 449 степеням свободы.

В нашем случае, строки именно для числа 449 нет, зато несложно заметить, что значения для 100 и 1000 — ближайших подходящих строк — отличаются на сотые доли, поэтому для большого числа степеней свободны подойдет любая строка.

Наше значение 2,0014 находится между 1,9623 и 2,3301: 1,9623 < 2,0014 < 2,3301

В шапке таблицы это соответствует 95%-му и 98%-му квантилю распределения Стьюдента, т. е. мы захватили 95%-й квантиль, но не захватили 98%-й:

Если расчетное значение t-критерия Стьюдента больше контрольного, значит, «альтернативная гипотеза» верна с соответствующей вероятностью (95%), и выборки статистически различаются.

Если бы мы получили значение t-критерия больше, чем 2,3301 (98%), мы бы могли говорить по правильности «альтернативной гипотезы» уже с 98%-й вероятностью. Аналогично, если бы мы получили значение t-критерия меньше, чем 1,9623 (95%), но больше 1,6464 (90%), мы бы говорили о правильности гипотезы на 90%.

Вывод: расчетное значение t-критерия Стьюдента 2,0014 соответствует, по меньшей мере, 95% уверенности в том, что между выборками есть статистически значимые различия, и звонки Асланян, действительно, в среднем длиннее звонков Евтушенко.

Наша «альтернативная гипотеза» получила 95%-ое подтверждение, мы можем быть уверены в результате и принимать решение о дальнейшей работе с полученный информацией.

Полезные ссылки

http://www.evanmiller.org/ab-testing/t-test.html