В статье «Кейс: заменили на Black Friday колл-центр KupiVIP роботом, и только 5 человек из 5000 поняли, что общаются с нейросетью» на vc.ru меня, среди прочего, не могла не заинтересовать фраза, где автор рассказывает о росте конверсии с 6% до 8%:

Естественно, я задумался, на каком же объеме звонков был зафиксирован данный рост конверсии, и достаточен ли был этот объем, чтобы можно было достоверно утверждать, что голосовой робот эффективнее живых операторов колл-центра.

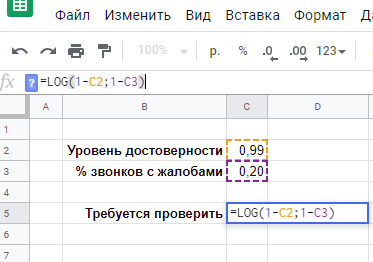
Точно вопрос можно было бы сформулировать, например, следующим образом: какой минимальный объем звонков требуется сделать, чтобы с уровнем достоверности, например, 95% зафиксировать рост конверсии с 6% до 8%?

Строим эксперимент в Excel

Попробуем выписать имеющиеся данные в Excel. Для дальнейших расчетов нам понадобится параметр «число звонков» — предположим пока, что и робот, и операторы сделали по 1000 звонков, прежде чем были получены конверсии 6% и 8%:

Вообще, налицо обычный А/Б сплит-тест, и далее нам нужно будет пройтись по его алгоритму для получения Z-оценки и расчета p-значения.

Рассчитаем стандартные ошибки (SD, или σ) для обеих конверсий и стандартную ошибку разницы этих конверсий. Формула для расчета стандартной ошибки конверсии:

где p — конверсия (6%, например), n — размер выборки (1000 звонков). Считаем в Excel:

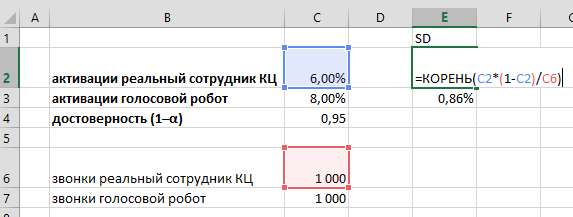
Стандартная ошибка разницы конверсий — считаем по формуле:

где σ — это стандартная ошибка каждой из конверсий A и B (оператор и робот). В Excel посчитаем ее чуть ниже:

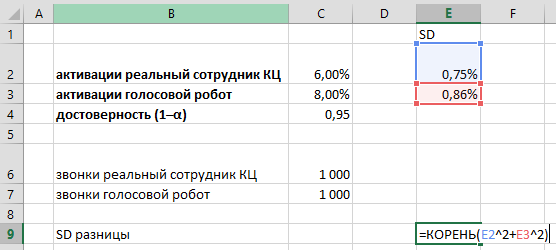
Насколько разница между конверсиями A и B больше, чем стандартная ошибка этой разницы? Это соотношение называется Z-оценкой. В Excel считается совсем просто:

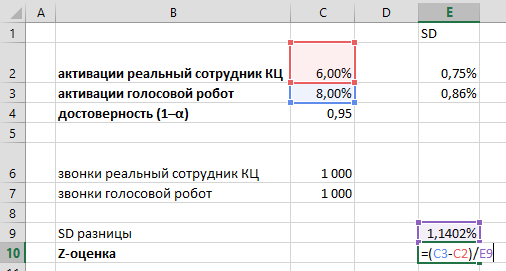
Итак, Z-оценка = 1,7541. На графике нормального распределения это соответствует 96%-му персентилю, то есть, вероятность, что Z-оценка случайно окажется выше 1,7541 составляет порядка 4% (иными словами, 96% площади под колоколом нормального распределения не выходят за пределы +1,7541 стандартных отклонений):

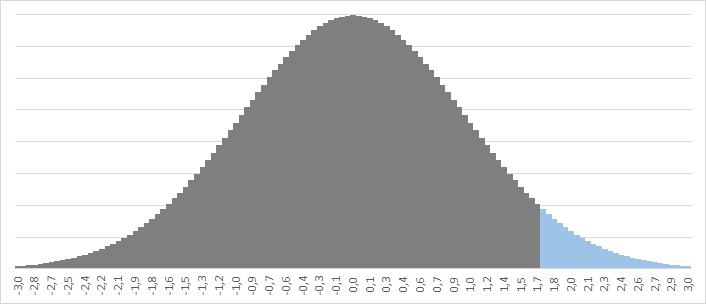
Откуда мы взяли именно 96%? Точное значение вероятности, p-значение, вычисляем по формуле:

=НОРМ.РАСП(1,7541;0;1;ИСТИНА)

P-значение = 96,03%.

Итак, промежуточный вывод: если на выборке в 1000 звонков в каждом из двух случаев мы обнаружили конверсии (активации промокода) в 6% и 8% звонков, то мы на 96% уверены, что эта разница не случайна. (Остается 4% вероятности, что обнаруженная разница — случайность. Тогда, возможно, конверсия вообще одинакова и равна, например, 7%. Сделай мы больше звонков, разница вскоре сошла бы на нет).

Эксперимент минимального размера

Однако, вернемся к первоначальной задаче.

Мы не хотели убедиться, что 8% больше, чем 6%, да и цифра 1000 звонков для робота и операторов была выбрана наугад. Мы хотели рассчитать минимальное количество звонков, чтобы с уровнем уверенности 95% зафиксировать статистическую значимость разницы между 8% и 6%.

1000 звонков нам оказалось точно достаточно. Теперь нам остается уменьшать это число до той поры, пока p-значение не пересечет границу 95%. (По формуле нормального распределения, кстати, это будет соответствовать Z-оценке, равной 1,6449 — попробуйте проверить.)

В теории, наверное, можно было бы вывести большую формулу для расчета такого n, при котором p-значение будет равно 0,95. На практике, быстрее окажется вручную подобрать минимальное n. Или, еще лучше, воспользоваться в Excel инструментом Данные — Анализ «что, если» — Подбор параметра:

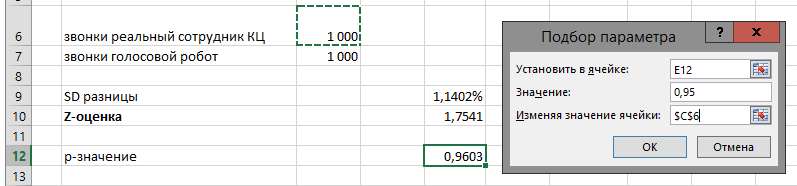
(Убедитесь только, что число звонков робота ровно то же самое, что и число звонков оператора, т. е. вы указали =C6 в ячейке C7).

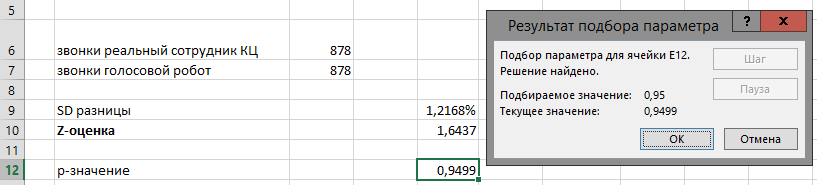
Выводы

Итак, мы вычислили минимальные условия эксперимента для оценки эффективности голосового робота для KupiVIP.

Нужно не менее 878 звонков в каждой из двух групп, чтобы с уровнем достоверности 95% подтвердить наличие разницы между 6% активаций промокодов в контрольной группе (реальные сотрудники) и 8% в тестовой группе (голосовой робот).

(Единственное, ни 6%, ни 8% не дают целого числа активаций на выборке из 878 звонков, и, в реальности, конечно, цифры будут другие, причем число звонков в двух группах вообще может быть различным. Но, на самом деле, это не имеет большого значения, т. к., наверняка, в статье были приведены округленные значения конверсий).

См. также:

https://abtestguide.com/calc/?ua=1000&ub=1000&ca=60&cb=80

На днях пришел в голову такой пример: предположим, подрядчик жалуется на плохую связь «в каждом пятом» звонке.

Наша задача проверить, справедлива ли гипотеза, что 20% звонков имеют проблемы со связью. Причем, как всегда, мы не просто сделаем 100 тестовых звонков (на это у нас нет ресурсов), а сформулируем нулевую гипотезу, альтернативную гипотезу, и проверим ее с заданным уровнем достоверности.

Выдвигаем гипотезу и определяем уровень достоверности

Нулевой гипотезой (H₀) пусть будет предположение, что со связью все в порядке, или, по крайней мере, проблемы встречаются реже, чем в 20% звонков.

Альтернативной гипотезой (H₁), которую мы будем проверять, пусть будет предположение подрядчика, что в каждом пятом звонке наблюдаются помехи. То есть, по крайней мере, в 20% звонков есть проблемы со связью.

Уровень достоверности — это наша уверенность в результатах эксперимента. Чем он выше, тем больше придется сделать проверочных звонков, поэтому мы заложим 1% на возможную ошибку, и выберем уровень достоверности в 99% (1%, что, если даже эксперимент не подтвердит проблем со связью, они, в действительности, могут быть).

Cобираем формулу для расчета выборки

Предположим, цель эксперимента — опровергнуть альтернативную гипотезу H₁ («есть проблемы»), подтвердив нулевую гипотезу H₀ («все в порядке»). Чтобы сделать это, нам будет достаточно продемонстрировать N подряд успешных звонков без признаков проблем со связью, при этом допуская вероятность, равную или меньше 1%, что нам просто повезет, и, при наличии, в действительности, проблем с оборудованием, они случайно не проявят себя ни в одном из N звонков.

Из предположения подрядчика вытекает, что 80% звонков не имеют проблем. Вероятность отсутствия сбоев в N звонках подряд равна 0,80^N. Нам нужно подобрать минимальное N, при котором вероятность упадет до 1%: 0,80^N = 1%

Получается, нам нужно вычислить логарифм 1% по основанию 80%!

Загружаем в Гугл Таблицы:

Формула для ячейки C5 будет выглядеть как

=LOG(1-C2;1-C3)

Нужно сделать 20,64 звонка. (Проверяем: 0,80^20,64 = 0,9995%, идеально.)

Остается только добавить округление:

=ОКРУГЛВВЕРХ(C5)

или сразу

=ОКРУГЛВВЕРХ(LOG(1-C2;1-C3))

Проверяем гипотезу

Если альтернативная гипотеза H₁ нашего подрядчика верна, и мы испытываем проблемы со связью в каждом пятом звонке, то, вероятность не заметить проблем в 21 тестовом звонке подряд составляет порядка 1%. Иными словами, либо это крайне редкое совпадение (1%), либо альтернативная гипотеза о проблемах в 20% звонков неверна (99%), и мы оставляем нулевую гипозеу H₀. С вероятностью 99% мы уверены, что проблем со связью не наблюдается.

Или вот еще был случай: разгар рабочего дня в отделе продаж, телефон молчит уже полчаса.

Варианта два: либо технический сбой, либо это просто случайно подзатянувшаяся пауза, и вот-вот поступит очередной звонок от клиента.

Попробуем разобраться, сколько минут можно просидеть в тишине, прежде чем надо начинать беспокоиться.

Неочевидный параметр телефонного звонка

Какими вообще параметрами обладает телефонный звонок в отделе продаж или в коллцентре? Дата и время, скорость ответа, длительность, день недели, номер линии, номер клиента — вот самые очевидные характеристики, по которым можно анализировать поступающие звонки.

Где-то в тени прячется еще один параметр — а именно, длительность паузы (промежутка без звонков), предшествующей очередному звонку. Например, звонок поступил в 14:07 13 февраля и продлился 3 мин 52 сек. Это то, что видно в выгрузке, в логах АТС или в CRM. Не менее любопытно, что, если предыдущий звонок был зарегистрирован в 14:01, то пауза в 6 минут является тем самым неочевидным параметром, который тоже можно было бы проанализировать.

Допустим, возьмем звонки в коллцентр в будние дни с 10 до 19 часов. Посчитаем разность в минутах между двумя соседними звонками — «0», если прошло меньше минуты, «1» — от одной до двух минут (от 01:00 до 01:59), и так далее. Проанализировав тысячи звонков, получаем примерно такую таблицу:

(Строго говоря, паузы более 40 минут тоже присутствуют, но их доля ничтожно мала, поэтому, округляя до десятых, мы достигаем 100% уже на 40 минутах.)

Простая идея «аномальных» пауз

Итого, мы имеем удивительно красивую гистограмму распределения длительности пауз между звонками. Что примечательно, длительности пауз убывают по экспоненте:

Вернемся к тому, что мы вообще хотели посчитать в самом начале.

У нас родилась идея, что рано или поздно, перерыв между звонками в середине рабочего дня становится таким длительным, что это начинает вызывать тревогу у менеджеров. Логично предположить, что в каждом отделе продаж или коллцентре тревогу вызывать будут затянувшиеся паузы разной длительности — для больших коллцентров перерыв в 5 минут это уже очень маловероятно, для других — 5 минут это стандартный промежуток между звонками, а вот 55 минут — уже очень подозрительно.

А что если попробовать сформулировать идею «аномально» затянувшейся паузы между звонками таким образом: это такая пауза, которая встречается чрезвычайно редко, например, раз в неделю, или раз в месяц, или раз в полгода. Определим для себя уровень «аномалии», кажущийся нам разумным, и посчитаем, паузы какой длительности встречаются примерно так редко, как мы определили нашу «аномалию».

Например, пусть аномальной будет считаться пауза, которая, в среднем, встречается раз в неделю.

Если в нашу таблицу длительностей пауз между звонками попали звонки за прошедший год, логично, что количество «аномальных» («раз в неделю») пауз там будет порядка 52 штук (по числу недель).

Итак, нам нужно отсчитать 52 звонка с самыми длительными паузами перед ними. В моей таблице нашлось 47 звонков с паузами 38+ минут, затем идут 57 звонков с паузами 37+ и более минут.

Таким образом, можно сделать вывод, что пауза в 37-38 минут между звонками в будний день должна настораживать: либо перед нами еженедельная «аномалия», наблюдаемся порядка 52 раз в год, либо речь идет о том, что мог произойти технический сбой, и звонки перестали поступать.